Independent set in discrete mathematicsThe independent set can be described as a set which contains the following details:
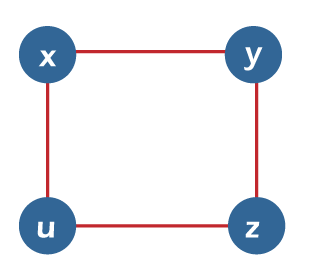 From the above graph, we have the following details of an independent set. I1= {x} I2 = {y} I3 = {z} I4 = {u} I5 = {x, z} I6 = {y, u} Therefore, the maximum number of non-adjacent vertices or independence number α0 (G) = 2. Independent line setSuppose there is a graph G = (V, E). If there is a subset L and no two edges in this subset are adjacent, in this case, the subset L of E will be known as the independent line set of G. The example of an independent line set is described as follows: 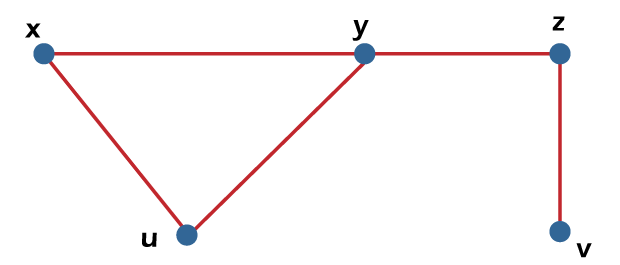 From the above graph, we will consider the following subset. L1= {x, y} L2 = {x, y} {z, v} L3 = {x, u} {y, z} In the above graph, we can see that subsets L2 and L3 do not contain the adjacent edges. Hence the subsets L2 and L3 are the independent line sets. But the subset L1 is not an independent line set because we can form an independent line set with the help of minimum of two edges, but in L1, there is only one edge. Hence we can say that the subset L1 is not an example of an independent line set. Maximal Independent line setThe maximal independent line set is also known as the maximal matching. An independent line set will be known as the maximal independent line set of G if there is no possibility to add any extra edge of G into subset L. The example of a maximal independent line set is described as follows: 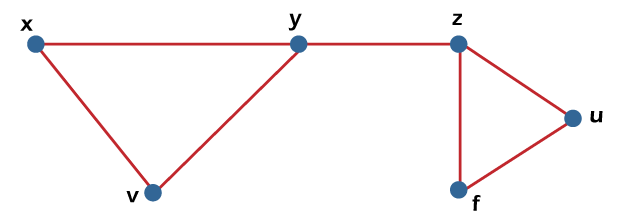 From the above graph, we will consider the following subset. L1= {x, y} L2 = {{y, v} {z, f}} L3 = {{x, v} {y, z}, {u, f}} L4 = {{x, y} {z, f}} The subsets L2 and L3 are the maximal independent line sets because, in the above graph, we can see that subsets L2 and L3 are not able to add any other edge which is not adjacent. Hence we can say that the subsets L2 and L3 are known as the maximal independent line sets. Maximum independent line setWe can calculate the maximum independent line set of G with the help of calculating the maximum number of edges in that graph. We can calculate the maximum independent line set with the help of following formula: Number of edges in a maximum independent line set of G (β1 ) = matching number of G = Line independent number of G The example of a maximum independent line set is described as follows:  From the above graph, we will get the following details about the subset. L1= {x, y} L2 = {{y, v} {z, f}} L3 = {{x, v} {y, z}, {u, f}} L4 = {{x, y} {z, f}} In the above graph, we can see that the subset L3 have the maximum edges and these edges are not adjacent. Hence the subset L3 can be called the maximum independent line set. The maximum independent line set of subset L3 can be represented like this: β1 = 3 Note: If there is a graph G which does not have an isolated vertex, then it will beα1 + β1 = number of vertices in a graph = |V| For example: In this example, we will show the line covering a number of Kn/Cn/Wn like this: 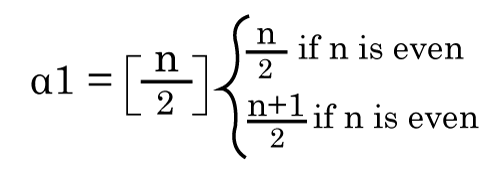 Line independent number = β1 = [n/2] α1 + β1 = n. Edge Covering
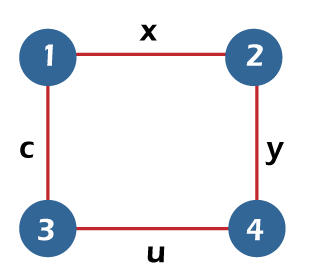 From the above graph, we have the following details of edge covering. E1= {x, y, z, u} E2 = {x, u} E3 = {y, z} Therefore, the edge covering number or the minimum number of edges that covers all the vertices β1 (G) = 2. Note: For a graph G, α1(G) + β1(G) = n, where n is used to indicate the number of vertices in G.Independent vertex setSuppose there is a graph G = (V, E). If there is a subset S in which no two vertices in this subset are adjacent, in this case, the subset S of V will be known as the independent vertex set of G. The example of an independent vertex set is described as follows: 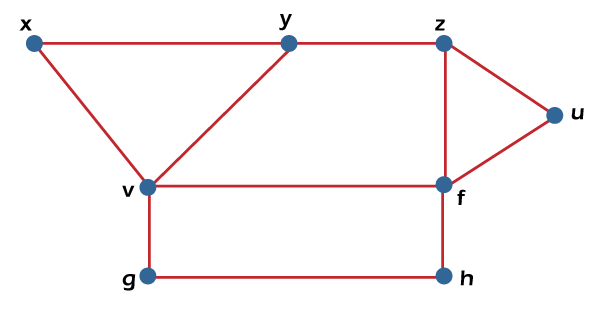 From the above graph, we will consider the following subset. S1= {v} S2 = {v, f} S3 = {x, g, z} S4 = {v, u} In the above graph, we can see that subsets S2, S3 and S4 do not contain any vertex that is adjacent to any other vertex. Hence we can say that the subsets S2, S3 and S4 are known as the independent vertex sets. But the subset S1 is not an independent vertex set because we can form an independent vertex set with the help of minimum two vertices, but in S1, there is only one vertex. Hence independent vertex set cannot be indicated by the subset S1. Maximal Independent Vertex setSuppose there is a graph G. The independent vertex set will be known as the maximal independent vertex set if there is a subset S, which does not have any possibility to add any other extra vertex of G into S, in this case, the independent vertex set will be known as the maximal independent vertex set. The example of an independent vertex set is described as follows: 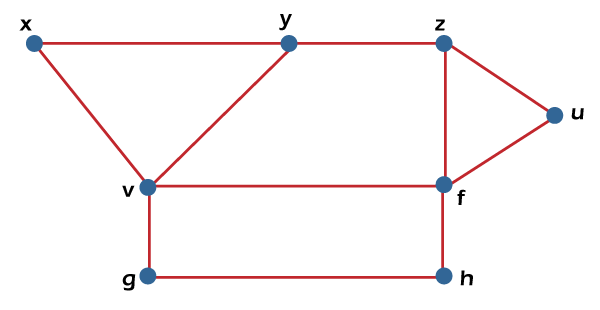 From the above graph, we will consider the following subset. S1= {v} S2 = {v, f} S3 = {x, g, z} S4 = {v, u} The subsets S2 and S3 are the maximal independent vertex sets because in the above graph, we can see that subsets L2 and L3 are not able to add any other vertex. Hence we can say that the subsets S2 and S3 are known as the maximal independent line sets. But subsets S1 and S4 are not the maximal independent vertex sets because we can add another vertex into it. Maximum Independent vertex setWe can calculate the maximum independent vertex set of G with the help of calculating the maximum number of vertices in that graph. The example of a maximum independent vertex set is described as follows: 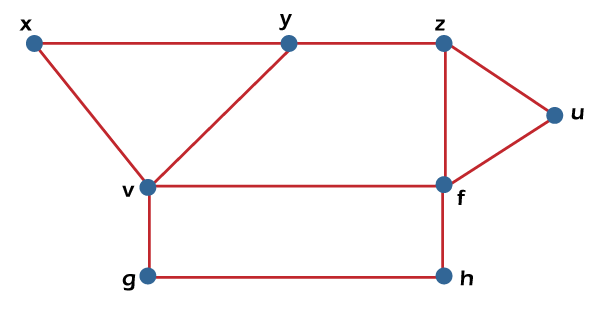 From the above graph, we will consider the following subset. S1= {v} S2 = {v, f} S3 = {x, g, z} S4 = {v, u} In the above graph, we can see that the subset S3 covers the maximum number of vertices. Hence we can say that the subset S3 is known as the maximum independent vertex set of G. In the maximum independent vertex set, the number of vertices can be known as the independent vertex number of G (β2). For example: If there is a complete graph Kn, then the vertex covering number and vertex independent number can be determined by the following formula: Vertex independent number = α2 = n−1 Vertex covering number = β2 = 1 So we have the following: α2 + β2 = n Each and every vertex of a complete graph will be adjacent to its remaining (n-1) vertices. Therefore, there will be only one vertex for a maximum independent set of Kn. Therefore, β2 = 1 and α2=|v| − β2 = n-1 Note: If there is a graph G = (V, E), then it will contain the following: |