Abstract
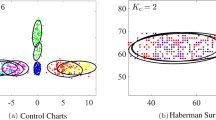
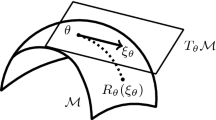
In many practical applications, the data is organized along a manifold of lower dimension than the dimension of the embedding space. This additional information can be used when learning the model parameters of Gaussian mixtures. Based on a mismatch measure between the Euclidian and the geodesic distance, manifold constrained responsibilities are introduced. Experiments in density estimation show that manifold Gaussian mixtures outperform ordinary Gaussian mixtures.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Parzen, E.: On estimation of a probability density function and mode. Ann. Math. Stat. 33, 1065–1076 (1962)
Vincent, P., Bengio, Y.: Manifold Parzen windows. In: Thrun, S., Becker, S., Obermayer, K. (eds.) NIPS 15, pp. 825–832. MIT Press, Cambridge (2003)
McLachlan, G.J., Peel, D.: Finite Mixture Models. Wiley, New York (2000)
Archambeau, C., Verleysen, M.: From semiparametric to nonparametric density estimation and the regularized Mahalanobis distance (2005) (submitted)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm (with discussion). J. Roy. Stat. Soc., B 39, 1–38 (1977)
Lee, J.A., Lendasse, A., Verleysen, M.: Nonlinear projection with curvilinear distances: Isomap versus Curvilinear Distance Analysis. Neurocomputing 57, 49–76 (2003)
Tenenbaum, J.B., de Silva, V., Langford, J.C.: A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000)
Bernstein, M., de Silva, V., Langford, J., Tenenbaum, J.: Graph approximations to geodesics on embedded manifolds. Techn. report Stanford University, CA (2000)
West, D.B.: Introduction to Graph Theory. Prentice-Hall, Upper Saddle River (1996)
Dijkstra, E.W.: A note on two problems in connection with graphs. Num. Math. 1, 269–271 (1959)
Xu, L., Jordan, M.I.: On convergence properties of the EM algorithm for Gaussian mixtures. Neural Comput. 8, 129–151 (1996)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Archambeau, C., Verleysen, M. (2005). Manifold Constrained Finite Gaussian Mixtures. In: Cabestany, J., Prieto, A., Sandoval, F. (eds) Computational Intelligence and Bioinspired Systems. IWANN 2005. Lecture Notes in Computer Science, vol 3512. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11494669_100
Download citation
DOI: https://doi.org/10.1007/11494669_100
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-26208-4
Online ISBN: 978-3-540-32106-4
eBook Packages: Computer ScienceComputer Science (R0)