Abstract
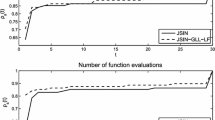
We propose a new derivative-free line search technique which contains the classical Li-Fukushima derivative-free line search [Optim. Methods Softw. 13 (3), 181–201, 2000] as a special case. The new line search can enable us to choose a larger step size at each iteration and reduce the number of function evaluations at each step. Based on the new line search, we prove that Broyden-like method for solving the nonlinear equation is globally and locally superlinearly convergent under appropriate assumptions. Moreover, we present some nonlinear equations arising from nonlinear complementarity problems (NCP), weighted linear complementarity problems (wLCP) and system of inequalities (SI). Numerical results show that Broyden-like method based on the new line search has better numerical performance than that based on Li-Fukushima line search.
Similar content being viewed by others
References
Asadi, S., Darvay, Z., Lesaja, G., Mahdavi-Amiri, N., & Potra, F. A. (2020). A full-Newton step interior-point method for monotone weighted linear complementarity problems. Journal of Optimization Theory and Applications, 186, 864–878.
Broyden, C. G. (1965). A class of methods for solving nonlinear simultaneous equations. Mathematics of Computation, 19, 577–593.
Chen, B., & Ma, C. (2011). A new smoothing Broyden-like method for solving nonlinear complementarity problem with a \(P_0\)-function. Journal of Global Optimization, 51, 473–495.
Chen, B., & Ma, C. (2011). Superlinear/quadratic smoothing Broyden-like method for the generalized nonlinear complementarity problem. Nonlinear Analysis: Real World Applications, 12, 1250–1263.
Chen, J. S. (2006). The semismooth-related properties of a merit function and adescent method for the nonlinear complementarity problem. Journal of Global Optimization, 36, 565–580.
Chen, J. S., & Pan, S. H. (2008). A family of NCP functions and a descent method for the nonlinear complementarity problem. Computational Optimization and Applications, 40, 389–404.
Chen, J. S., Ko, C. H., Liu, Y. D., & Wang, S. P. (2016). New smoothing functions for solving a system of equalities and inequalities. Pac. J. Optim., 12(1), 185–206.
Cheng, W. Y., & Li, D. H. (2009). A derivative-free nonmonotone line search and its application to the spectral residual method. IMA Journal of Numerical Analysis, 29, 814–825.
Chi, X. N., Gowda, M. S., & Tao, J. (2019). The weighted horizontal linear complementarity problem on a Euclidean Jordan algebra. Journal of Global Optimization, 73, 153–169.
Dennis, J. E., Jr., & Moré, J. J. (1977). Quasi-Newton methods, motivation and theory. SIAM Review, 19, 46–89.
Diniz-Ehrhardta, M. A., Martíneza, J. M., & Raydan, M. (2008). A derivative-free nonmonotone line-search technique for unconstrained optimization. Journal of Computational and Applied Mathematics, 219, 383–397.
Facchinei, F., & Pang, J. S. (2003). Finite-dimensional variational inequalities and complementarity problems. New York: Springer.
Fan, B. (2015). A smoothing Broyden-like method with a nonmonotone derivative-free line search for nonlinear complementarity problems. Journal of Computational and Applied Mathematics, 290, 641–655.
Fan, X., & Yan, Q. (2019). Solving system of inequalities via a smoothing homotopy method. Numerical Algorithms, 82, 719–728.
Ferris, M. C., & Pang, J.-S. (1997). Engineering and economic applications of complementarity problems. SIAM Review, 39(4), 669–713.
Gowda, M. S. (2019). Weighted LCPs and interior point systems for copositive linear transformations on Euclidean Jordan algebras. Journal of Global Optimization, 74(4), 285–295.
Griewank, A. (1986). The “global’’ convergence of Broyden-like methods with suitable line search. The ANZIAM Journal, 28, 75–92.
Grippo, L., & Rinaldi, F. (2015). A class of derivative-free nonmonotone optimization algorithms employing coordinate rotations and gradient approximations. Computational Optimization and Applications, 60, 1–33.
La Cruz, W., Martinez, J. M., & Raydan, M. (2006). Spectral residual method without gradient information for solving large-scale nonlinear systems of equations. Mathematics of Computation, 75(255), 1429–1448.
La Cruz, W., Martinez, J.M., Raydan, M. (2004). Spectral residual method without gradient information for solving large-scale nonlinear systems: Theory and experiments, Technical Report RT-04-08, Dpto. de Computacion, UCV, Available at www.kuainasi.ciens.ucv.ve/ccct/mraydan\(_{-}\)pub.html.
Li, D. H., & Fukushima, M. (1999). A globally and superlinearly convergent Gauss-Newton-based BFGS method for symmetric nonlinear equations. SIAM Journal on Numerical Analysis, 37(1), 152–172.
Li, D. H., & Fukushima, M. (1999). A derivative-free line search and DFP method for symmetric equations with global and superlinear convergence. Numerical functional analysis and optimization, 20, 59–77.
Li, D. H., & Fukushima, M. (2000). A derivative-free line search and global convergence of Broyden-like method for nonlinear equations. Optimization methods and software, 13(3), 181–201.
Li, D. H., & Fukushima, M. (2000). Smoothing Newton and quasi-Newton methods for mixed complementarity problems. Computational Optimization and Applications, 17, 203–230.
Li, D. H., & Fukushima, M. (2001). Globally convergent Broyden-like methods for semismooth equations and applications to VIP. Annals of Operations Research Annals of Operations Research, 103, 71–79.
Li, D. H., & Fukushima, M. (2001). A modified BFGS method and its global convergence in nonconvex minimization. Journal of Computational and Applied Mathematics, 129, 15–35.
Li, D. H., & Fukushima, M. (2001). On the global convergence of BFGS method for nonconvex unconstrained optimization problems. SIAM Journal on Optimization, 11, 1054–1064.
Li, D. H., Yamashita, N., & Fukushima, M. (2001). Nonsmooth equation based BFGS method for solving KKT systems in mathematical programming. Journal of Optimization Theory and Applications, 109(1), 123–167.
Li, Y. F., Sun, G., & Wang, Y. J. (2011). A smoothing Broyden-like method for polyhedral cone constrained eigenvalue problem. Numerical Algebra, Control & Optimization, 1(3), 529–537.
Ma, C. F., Chen, L., & Wang, D. (2008). A globally and superlinearly convergent smoothing Broyden-like method for solving nonlinear complementarity problem. Applied Mathematics and Computation, 198, 592–604.
Potra, F. A. (2012). Weighted complementarity problems-a new paradigm for computing equilibria. SIAM Journal on Optimization, 22(4), 1634–1654.
Powell, M.J.D. (1970). A fortran subroutine for solving systems of nonlinear algebraic equations. In: Rabinowitz, P. (Ed.), Numerical methods for nonlinear algebraic equations. Gordon and Breach, London (Chapter 7)
Tang, J. Y., & Zhang, H. C. (2021). A nonmonotone smoothing Newton algorithm for weighted complementarity problems. Journal of Optimization Theory and Applications, 189, 679–715.
Tang, J. Y., & Zhou, J. C. (2021). Quadratic convergence analysis of a nonmonotone Levenberg-Marquardt type method for the weighted nonlinear complementarity problem. Computational Optimization and Applications, 80, 213–244.
Tang, J. Y., & Zhou, J. C. (2021). A modified damped Gauss-Newton method for non-monotone weighted linear complementarity problems. Optim. Methods Softw.https://doi.org/10.1080/10556788.2021.1903007
Tang, J. Y., & Zhou, J. C. (2021). A smoothing quasi-Newton method for solving general second-order cone complementarity problems. Journal of Global Optimization, 80, 415–438.
Tang, J. Y., & Zhou, J. C. (2020). Smoothing inexact Newton method based on a new derivative-free nonmonotone line search for the NCP over circular cones. Annals of Operations Research, 295, 787–808.
Tang, J., & Liu, S. Y. (2010). A new smoothing Broyden-like method for solving the mixed complementarity problem with a \(P_0\)-function. Nonlinear Analysis: Real World Applications, 11, 2770–2786.
Zhou, W. J., & Zhang, L. (2020). A modified Broyden-like quasi-Newton method for nonlinear equations. Journal of Computational and Applied Mathematics, 372, 112744.
Acknowledgements
Research of this paper was partly supported by National Natural Science Foundation of China (11771255), Young Innovation Teams of Shandong Province (2019KJI013), Natural Science Foundation of Henan Province (222300420520) and Key scientific research projects of Higher Education of Henan Province (22A110020). We are very grateful to the two referees for their valuable comments on the paper which have considerably improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tang, J., Zhou, J. & Sun, Z. A derivative-free line search technique for Broyden-like method with applications to NCP, wLCP and SI. Ann Oper Res 321, 541–564 (2023). https://doi.org/10.1007/s10479-022-04796-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-022-04796-z