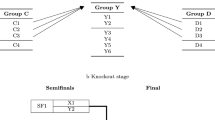
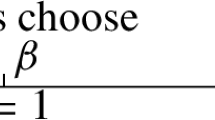Abstract
This article focuses on the question of whether a certain candidate’s (player’s) chance to advance further in a tennis tournament can be increased when the ordering of the tournament can be controlled (manipulated by the organizers) according to his own preferences. Is it possible to increase the number of ranking points a player will receive? And most importantly, can it be done in reasonable computational time? The answers to these questions differ for different settings. e.g., the information available on the outcome of each game, the significance of the number of points gained or of the number of games won. We analyzed five different variations of these tournament questions. First the complexity hardness of trying to control the tournaments is shown. Then, the tools of parametrized complexity are used to investigate the source of the problems’ hardness. Specifically, we check whether this hardness holds when the size of the problem is bounded. The findings of this analysis show that it is possible under certain circumstances to control the tournament in favor of a specific candidate in order to help him advance further in the tournament.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Abboud, A., Lewi, K., Williams, R.: Losing weight by gaining edges European Symposium on Algorithms, pp 1–12. Springer (2014)
Arrow, K.J., Sen, A., Suzumura, K.: Handbook of social choice and welfare, vol.2. Elsevier (2010)
Aziz, H., Brill, M., Fischer, F., Harrenstein, P., Lang, J., Seedig, H. G.: Possible and necessary winners of partial tournaments. J. Artif. Intell. Res. 54, 493–534 (2015)
Aziz, H., Gaspers, S., Mackenzie, S., Mattei, N., Stursberg, P., Walsh, T.: Fixing a balanced knockout tournament. In: AAAI, pp 552–558 (2014)
Bartholdi, J.J., Tovey, C.A., Trick, M.A.: The computational difficulty of manipulating an election. Soc. Choice Welf. 6(3), 227–241 (1989)
Bartholdi, J.J., Tovey, C.A., Trick, M.A.: How hard is it to control an election? Math. Comput. Model. 16(8-9), 27–40 (1992)
Betzler, N., Uhlmann, J.: Parameterized complexity of candidate control in elections and related digraph problems. Theor. Comput. Sci. 410(52), 5425–5442 (2009)
Brams, S.J., Fishburn, P.C., Arrow, K.J., Sen, A.K., Suzumura, K.: Handbook of social choice and welfare (2002)
Chen, J., Faliszewski, P., Niedermeier, R., Talmon, N.: Elections with few voters: Candidate control can be easy. In: AAAI, pp 2045–2051 (2015)
Cormen, T.H.: Introduction to algorithms. MIT press (2009)
Downey, R.G., Fellows, M.R.: Fixed-parameter tractability and completeness II: On completeness for w [1]. Theor. Comput. Sci. 141(1-2), 109–131 (1995)
Downey, R.G., Fellows, M.R.: Parameterized complexity. Springer Science & Business Media (2012)
Erdélyi, G., Fellows, M.R., Rothe, J., Schend, L.: Control complexity in bucklin and fallback voting: An experimental analysis. J. Comput. Syst. Sci. 81(4), 661–670 (2015)
Erdélyi, G., Fernau, H., Goldsmith, J., Mattei, N., Raible, D., Rothe, J.: The complexity of probabilistic lobbying. In: International Conference on Algorithmic DecisionTheory, pp 86–97. Springer (2009)
Faliszewski, P., Hemaspaandra, E., Hemaspaandra, L.A., Rothe, J.: Copeland voting fully resists constructive control. In: International Conference on Algorithmic Applications in Management, pp 165–176. Springer (2008)
Fellows, M.R., Koblitz, N.: Fixed-parameter complexity and cryptography. In: International Symposium on Applied Algebra, Algebraic Algorithms, and Error-Correcting Codes, pp 121–131. Springer (1993)
Flum, J., Grohe, M.: Parameterized complexity theory, volume xiv of texts in theoretical computer science. an eatcs series (2006)
Gary, M.R., Johnson, D.S.: Computers and intractability: A guide to the theory of np-completeness (1979)
Hazon, N., Dunne, P.E., Kraus, S., Wooldridge, M.: How to rig elections and competitions. Proc. COMSOC (2008)
Horen, J., Riezman, R.: Comparing draws for single elimination tournaments. Oper. Res. 33(2), 249–262 (1985)
Kim, M.P., Suksompong, W., Williams, V.V.: Who can win a single-elimination tournament? arXiv:1511.08416 (2015)
Lang, J., Pini, M.S., Rossi, F., Salvagnin, D., Venable, K.B., Walsh, T.: Winner determination in voting trees with incomplete preferences and weighted votes. Auton. Agent. Multi-Agent Syst. 25(1), 130–157 (2012)
Mattei, N., Goldsmith, J., Klapper, A., Mundhenk, M.: On the complexity of bribery and manipulation in tournaments with uncertain information. J. Appl. Log. 13(4), 557–581 (2015)
Moulin, H., Brandt, F., Conitzer, V., Endriss, U., Lang, J., Procaccia, A.D.: Handbook of Computational Social Choice. Cambridge University Press (2016)
Russell, T., Walsh, T.: Manipulating tournaments in cup and round robin competitions. In: International Conference on Algorithmic DecisionTheory, pp 26–37. Springer (2009)
Sandholm, T.W.: Distributed rational decision making. Multiagent systems: a modern approach to distributed artificial intelligence (1999)
Vu, T., Altman, A., Shoham, Y.: On the agenda control problem in knockout tournaments. Proc. COMSOC (2008)
Vu, T., Altman, A., Shoham, Y.: On the complexity of schedule control problems for knockout tournaments. In: Proceedings of The 8th International Conference on Autonomous Agents and Multiagent Systems-Volume 1, pp. 225–232 International Foundation for Autonomous Agents and Multiagent Systems (2009)
Vu, T.D., Shoham, Y., Jackson, M.O., Roughgarden, T.: Knockout tournament design: a computational approach. Stanford University (2010)
Walsh, T.: Is computational complexity a barrier to manipulation? Ann. Math. Artif. Intell. 62(1-2), 7–26 (2011)
Williams, V.V.: Fixing a tournament. In: Proceedings of AAAI (2010)
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Aronshtam, L., Cohen, H. & Shrot, T. Tennis manipulation: can we help serena williams win another tournament?. Ann Math Artif Intell 80, 153–169 (2017). https://doi.org/10.1007/s10472-017-9549-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10472-017-9549-7