Abstract
During the last five decades, manufacturing has radically changed not only due to the technology development but also because of the new market and environmental requirements. Nowadays, companies are focused not only on cost-reduction and effectiveness or realized processes but also on reducing the negative impact on natural and social environment. Therefore, the maintenance is also transforming its role in order to better support value creation, both contributing to the economic dimension as well as extending its care for the environmental and social aspects. The paper presents a new method to solve the problem of the initial maintenance indicator merge into a new synthetic index that allows measuring the level of maintenance sustainability. The proposed approach allows to look at the process of combining indicators from a different perspective (i.e. through interactions between criteria) to help decision-makers in improving economic, social and environmental results of maintenance system. To justify effectiveness of proposed approach, it was applied to Composite Maintenance Sustainability Indicator, which was therefore generalized and expanded, so that it could be used in decision support system. The included case study shows the real benefit of using the proposed approach to analyse the actual results of maintenance system from sustainability point of view and forecasting future actions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Sustainable Manufacturing is defined as ‘the creation of manufactured products that use processes that minimize negative environmental impacts, conserve energy and natural resources, are safe for employees, communities and consumers, and are economically sound’ (ITA 2007). The goal of sustainable manufacturing is to obtain balance between environmental, social and economic dimensions in order to meet stakeholder requirements (Flammer 2013) and achieve a competitive advantage (Kannegiesser and Günther 2014). One of the means by which to achieve economic development, social progress and environmental quality presented in literature is the use and integration of the management standards such as: ISO 9001 requirements (Quality Management System), the ISO 45,001 (Occupational Health and Safety Management System) and the ISO 14,001 (Environmental Management System) and develop measures to assess sustainable manufacturing performance (Satolo et al. 2016).
The issue of performance measurement and manufacturing systems assessment from the sustainable development perspective is becoming more and more important for both the scientific community and practitioners (Shin et al. 2017; Machado et al. 2020). Moldavska and Velo (2019) implement sustainability assessment as the means to get a comprehensive and reliable analysis of current sustainability performance of manufacturing organization that enables identification of improvement areas.
In the industrial scope, one of the key areas that directly influences manufacturing sustainability of each company is the maintenance (e.g.; Savino et al. 2015, Li et al. 2020). According to EN 13,306:2017 standard maintenance is a ‘combination of all technical, administrative and managerial activities during the lifecycle of an object, aimed at maintaining or restoring the state in which an object can perform its functions’. Usually, maintenance activities are perceived as a supporting process for main processes performed in a company, provided for one customer only—production (Wang et al. 2020). According to this approach, maintenance is a cost. Meanwhile, complexity of contemporary manufacturing systems and their dependency on numerous internal and external factors has raised the interest of an increasing number of stakeholders in maintenance results. These results are perceptible not only in economic (increase or decrease of financial expenditures), but also in environmental (e.g., spare parts and consumable use, media use) and social dimensions (e.g., health and safety of employees).
Recently, sustainability in maintenance management has attracted much attention from both researchers and practitioners (Franciosi et al. 2017; Maletič et al. 2018; Singh and Gupta 2020; Boral et al. 2019; Franciosi et al. 2020a). Through innovative management practices, incorporating sustainability goals into maintenance management strategies and utilizing the potential available through new Maintenance 4.0 technologies at all stages of the machine’s life cycle, maintenance should and can contribute to promoting sustainable development (Bilge et al. 2017; Bokrantz et al. 2017; Chen et al. 2018; Franciosi et al. 2018; Macchi et al. 2018; Jasiulewicz-Kaczmarek and Gola 2019; Franciosi 2020b; Bevilacqua et al. 2020).
Therefore, the need to include sustainability issues in the assessment of maintenance results as support in meeting the challenges of sustainable manufacturing has been emphasized in the scientific literature. Some authors have considered specific sustainability perspectives in developing maintenance performance management system. Raouf (2009) introduced some indicators for a maintenance performance measurement system, which related to economic and environmental performance. Costantino et al. (2013) proposed a method to prioritize failures and schedule maintenance activities, considering environmental criticality of their consequences. Wu et al. (2012) proposed the use of a fuzzy multi-criteria decision-making process for the maintenance workforce performance analysis. Later, Sénéchal and Trentesaux (2019) provided a framework for decision-making on the maintenance of cyber physical systems based on the assessment of their environmental impact in terms of energy consumption and pollution. Some researchers have constructed a sustainable maintenance performance measurement system, which considered three sustainability perspectives. Sari et al. (2015), based on Balance Scorecard (BSC) model, developed an original structure for evaluating sustainable maintenance performance for automotive companies which consists of eight perspectives assigned to three dimensions of sustainability, with 15 quantities at the strategic echelon and 20 quantities at the tactic echelon as well as 43 quantities at the operative echelon. Pires et al. (2016) introduced an approach to the identification and prioritization of sustainability attributes (Triple Bottom Line (TBL) approach) identified in the Global Reporting Initiatives Guidelines (GRI) in relation to maintenance based on the Overall Equipment Efficiency (OEE) model Amrina and Yulianto (2018) proposed twelve Key Performance Indicators (KPI) of sustainable maintenance evaluation in the rubber industry assigned to three dimensions of sustainable development. An Interpretive Structural Modelling (ISM) analysis was then applied to show the relationship between the identified indicators. Jasiulewicz-Kaczmarek and Żywica (2018) developed performance assessment model, which integrate three sustainability dimensions (economic, social, and environmental) with four Kaplan and Norton’s balance scorecard perspectives (financial, client, internal processes and learning & growth). The model consists of two inference levels, the first one encompassing the assessment perspectives and the other including the assessment criteria. Singh and Gupta (2020) identified fourteen maintenance factors for sustainable performance improvement. By using ISM and fuzzy MICMAC (Matriced’ Impacts Croisés Appliquée á un Classement) the authors developed a framework for sustainable performance improvement and ranking the major driving factors by Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) approach. Recently, Franciosi et al. (2020a) developed holistic conceptual framework for measuring maintenance impacts on sustainability. In this framework, three dimensions of sustainability and impacts of maintenance on different areas of the organisation up to the customer were considered.
The literature review shows a number of research contributions aiming to define the impact of maintenance on taking on challenges of sustainable production. In general, most of these studies are focused on developing measures and indicators for sustainable maintenance assessment, and on designing assessment models (e.g. aggregate functions) which to a greater or lesser extent would take into account the relationships and dependencies between the assessment criteria.
The main goal of maintenance sustainability assessment is to provide decision makers with information about current maintenance results and support them in the decision-making process regarding future directions of maintenance activities improvement (e.g. which of the maintenance areas should be improved first and which can be dealt with later). Unfortunately, there is still a lack of comprehensive models in the literature to support decision-makers in assessing the results of decisions made in terms of contribution to sustainable development. In particular, to the knowledge of the authors, no systems have been developed to support decision-makers in the decision-making process of improving maintenance in relation to the dimensions of sustainable development (environment, social and economic).
In this context, the research gap that can be identified in studies conducted in the considered area concerns decision problems related to defining priorities of maintenance improvement action in the context of challenges of sustainable production. The proposed approach provides a framework for searching for possible maintenance improvement project completion scenarios, which allow to reach the maintenance sustainability target level.
Problem statement
The research presented is focused on expanding the existing model for assessing the sustainability of maintenance by introducing additional possibilities of use, mainly in decision support systems. Their implementation is to contribute to the answer to two main research questions:
-
RQ1. Which criteria limit the entire model, i.e. even a small decrease in their value will significantly affect the entire result? Similarly, it is important to determine which criteria should be invested in in the first place, so that the index value will increase to the greatest extent.
-
RQ2. How to fine-tune the model for the needs of a given enterprise, based on detailed data obtained from group of experts?
The main purpose of this work is to present a non-aggregative combination method of various decision indicators into a new one, preserving the character of the original models. Subject of the research is the Composite Maintenance Sustainability Index (CMSI) model presented in (Jasiulewicz-Kaczmarek and Żywica 2018).
The paper is organized as follows. ‘The framework of maintenance sustainability performance assessment’ section describes model of Composite Maintenance Sustainability Index (CMSI) and introduces methods and tools implemented in the model presented. ‘Extension of CMSI model for decision support system’ section presents extension of CMSI model for decision support system. The next section ‘Evaluation of the proposed model’ presents results of provided numerical experiments and discussion, whereas section ‘Conclusion’ discusses conclusions and further research directions.
The framework of maintenance sustainability performance assessment
Maintenance sustainability issues
According to Sénéchal (2018) ‘The maintenance activity is by nature an important lever for action on the sustainability of production systems’. Iung and Levrat (2014) pointed out that ‘maintenance as part of the circular economy can be considered, first, as an enabling system to sustain the artefact throughout its life cycle, then as a key tool to keep the regeneration potential of this artefact, and finally, as a target system that must be sustainable’. Based on literature review maintenance contribution to business competitive priorities and more sustainable manufacturing processes has two main dimensions.
The first dimension of maintenance contribution to a more sustainable production system is life cycle thinking represented by three life-cycle phases: beginning of life (BOL), middle of life (MOL) and end of life (EOL). Life cycle thinking means that people have a life cycle model in mind that affects the scope of their activities. A life cycle perspective for products and manufacturing assets is often mentioned in the literature regarding sustainability (Seliger et al. 2008). The goal of this approach is to understand and analyse individual stages of the life cycle, identify potential economic, social and environmental risk factors and opportunities at each stage, and create opportunities to take advantage of these opportunities and reduce potential risks. By the definition maintenance is a ‘combination of all technical, administrative and managerial activities during the lifecycle of an object, aimed at maintaining or restoring the state in which an object can perform its functions’ (EN 13306:2017). Thus, maintenance activities must be considered in all phases of the life cycle of the machine. From sustainable manufacturing perspective, the focus is on the possible integration of sustainability aspects into the activities in different life cycle phases (Marquez 2007; Jasiulewicz-Kaczmarek and Gola 2019; Meng et al. 2020):
-
1.
Identification of sustainability benefits that can be achieved in the phase of investment in new manufacturing equipment.
-
2.
Development of adequate maintenance strategies and a system for measuring the effectiveness of the use of manufacturing equipment at the stage of its operation, taking into account not only economic aspects but also environmental and social aspects.
-
3.
Integration of sustainability aspects in the end of life phase of a machine.
Considering the above, the traditional scope of maintenance operations limited only to the use phase of machines was extended to the remaining phases of the cycle (BOL and EOL) and has prompted the redefinition of the maintenance role as being ‘a prime method for life cycle management whose objective is to provide society with the required functions while minimizing material and energy consumption’ (Takata et al. 2004).
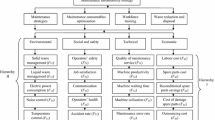
The second dimension of maintenance contribution to a more sustainable manufacturing system is represented by three sustainability aspects: economic, environmental and social (Fig. 1).
The contribution of maintenance processes in sustainable manufacturing (Jasiulewicz-Kaczmarek and Gola 2019)
Regarding the economic aspect of maintenance contribution in sustainable manufacturing, there are four relevant economic factors affected by the maintenance function: (1) quality and productivity; (2) delivery on time; (3) innovation: (4) cost (Jasiulewicz-Kaczmarek 2019). With reference to the social aspects, according to (Fraser et al. 2015), in maintenance management, ‘social implications’ should be made ‘mandatory’ instead of ‘if applicable’. Social sustainability of maintenance processes involves wider social benefits that can be derived from delivering high quality maintenance services. This means investing to maximize contributions to people’s health and safety, development of their competences, satisfaction from work, etc. Finally, environmental sustainability can be achieved by resource efficiency (water, air, energy, spare parts and materials), prevention of environmental damage, emission reductions and land conservation (Bokrantz et al. 2019). Depending on the specific operational context, these would require involvement of the maintenance function. These three aspects of maintenance contribution in sustainable manufacturing are interrelated and any change in any aspects highly influences the other two aspects (Fig. 2).
General model of interdependencies in sustainable maintenance (Jasiulewicz-Kaczmarek 2013)
Transition to sustainable maintenance requires changes in the way decisions are made, from a traditional approach based primarily on financial aspects to a more holistic approach that includes social and environmental aspects. It is a continuous process, which requires: (1) assessing the current sustainability maintenance performance; (2) identification of the improvement areas; (3) suggesting specific actions and (4) implementation of these actions. Based on the overall assessment of the maintenance system, the maintenance manager must answer the following questions: Are the results achieved satisfactory, or is it justified to undertake further improvement actions, in which areas should these actions be implemented?
Notation and definitions
Notation
- \( n \) :
-
number of criteria in the model
- \( X = \left\{ {x_{1} , \cdots ,x_{n} } \right\} \) :
-
the set of all criteria
- \( \left| X \right| \) :
-
cardinality of set \( X \), number of elements in \( X \)
- \( {\mathcal{P}}\left( X \right) \) :
-
power set of \( X \), set of all subsets of \( X \)
- \( \emptyset \) :
-
empty set
- \( \mu , \) :
-
Fuzzy measure,
- \( \lambda \) :
-
Unique parameter for Lambda fuzzy measure
- \( \mu_{\lambda } \) :
-
Discrete Sugeno \( \lambda \)-measure
- \( C_{\mu } \) :
-
Discrete Choquet integral with respect to fuzzy measure \( \mu \)
- \( v_{i} \) :
-
Shapley value for \( i \)-th criteria
- \( I_{i,j} \) :
-
Interaction Index of \( i \)-th and \( j \)-th criteria
- \( {\text{Agg}} \) :
-
Aggregation operator
- OWA:
-
Ordered Weighted Average
The fuzzy set theory has been applied to many problems in different fields of science and engineering. To describe this theory, some definitions are presented as follows:
Let \( X = \left\{ {x_{1} , \ldots , x_{n} } \right\} \) be the set of all criteria and \( {\mathcal{P}}\left( X \right) \) the power set of X.
Definition 1
(Fuzzy measure, Choquet 1954): A discrete fuzzy measure on X is a set function µ: \( {\mathcal{P}}\left( X \right) \) → [0, 1] satisfying the following conditions:
-
1.
µ(∅) = 0, µ(X) = 1,
-
2.
if A \( \subseteq \) B \( \subseteq \) X then μ(A) ≤ μ(B) (monotonicity).
In this context, μ(A) represents the degree of importance of given criteria set A. This way, additionally to the weight of a single criterion, the weight of an arbitrary criteria combination is also directly described. Fuzzy measure is additive when if \( A \cap B = \emptyset {\text{then}} \mu \left( {A \cup B} \right) = \mu \left( A \right) + \mu \left( B \right) \) and superadditive (subsdditive) when \( \mu \left( {A \cup B} \right) > \mu \left( A \right) + \mu \left( B \right) \) (respectively \( \mu \left( {A \cup B} \right) < \mu \left( A \right) + \mu \left( B \right)). \)
Definition 2
(Discrete Sugeno λ-measure) A discrete fuzzy measure is called Sugeno λ-measure if it satisfies:
-
3.
$$ {\text{If}}\;A \cap B\; = \;\emptyset ,\; {\text{then}}\; \mu_{\lambda } \left( {A \cup B} \right)\; = \;\mu_{\lambda } \left( A \right) + \mu_{\lambda } \left( B \right) + \lambda \mu_{\lambda } \left( A \right)\mu_{\lambda } \left( B \right) $$
-
4.
To differentiate this measure from other fuzzy measures, λ-fuzzy measure is denoted by µλ. Sugeno (1974) proved that given those 3 axioms, a fuzzy measure can be uniquely determined using only n = |X| coefficients µi that are often called fuzzy densities that represent the degree of importance of criteria i-th and can be calculated by parametric or nonparametric methods. The λ-measure can be calculated using the following formula:
$$ \mu_{\lambda } \left( {\left\{ {x_{1} , x_{2} , \ldots , x_{n} } \right\}} \right) = \left| {\mathop \sum \limits_{i = 1}^{n} \mu_{i} + \lambda \mathop \sum \limits_{{i_{1} = 1}}^{n - 1} \mathop \sum \limits_{{i_{2} = i_{1} + 1}}^{n} \mu_{{i_{1} }} \mu_{{i_{2} }} + \lambda^{n - 1} \mu_{1} \mu_{2} \ldots \mu_{n} } \right| = \frac{1}{\lambda }\left| {\mathop \prod \limits_{i = 1}^{n} \left( {1 + \lambda \mu_{i} } \right) - 1} \right| \quad {\text{for}} - 1 \le \lambda \le \infty $$(1)
Based on the boundary condition in Eq. (1), µλ(X) = 1, λ can be uniquely determined via the following equation:
where µi = µ({xi}), i = 1, 2, …, n is known as the fuzzy density function of a single element (singleton), xi \( \in X \).
Definition 3
(Discrete Choquet integral) Let µ be a discrete fuzzy measure on X. The discrete Choquet integral of function \( f:X \to \left[ {0,1} \right] \) with respect to fuzzy measure µ is defined by:
where: \( f_{\left( i \right)} \) indicates that the indices have been permutated so that \( 0 \le f_{\left( 1 \right)} \le \ldots \le f_{\left( n \right)} \le 1, \)
Definition 4
(Shapley value—\( \nu_{i} \), Murofushi 1992) Let µ be a fuzzy measure on X. The Shapley value (or the importance index) for every element xi \( \in X \) is defined by the following formula
where:
The Shapley value with respect to measure µ is a vector \( \nu = \left[ {\nu_{1} ,\nu_{2} , \ldots ,\nu_{n} } \right] \). It describes the global importance of every element by considering the effects of all subsets with and without the given element. According to the definition, the Shapley value has the property that the sum of all its components is 1, which can be formulated as \( \mathop \sum \limits_{i = 1}^{n} \nu_{i} = 1 \). Scaled by a factor n, the Shapley values greater than 1 indicate that the given element (criterion) is more important than the average.
Definition 5
(Interaction Index—\( I_{i,j} \), Murofushi and Soneda 1993) Let µ be a fuzzy measure on X. The interaction index of criteria xi and xj is defined by
The interaction index takes values from [-1, 1] interval, where negative (positive) values indicate negative (positive, synergic) interaction.
Definition 6
(Generalized Interaction index—\( I_{\mu } \left( T \right) \), Grabisch 1997) Let µ be a fuzzy measure on X. Generalized Interaction index of set of criteria \( T \subset X \) is defined by
where:
Note that this definition is consistent with previous ones, since we recover the Shapley value \( \nu_{i} \) for T = {xi}, and the interaction index \( I_{i,j} \) for \( T = \left\{ {x_{i} , x_{j} } \right\} \). Moreover, according to Grabisch (1997) each discrete fuzzy measure can be one-to-one represented by its Generalized Interaction Index
Definition 7
(k-additive fuzzy measure, Grabisch 1997) A discrete fuzzy measure is k-additive if for all \( T \subset X \) such that \( \left| T \right| > k {\text{we have}} I_{\mu } \left( T \right) = 0. \)
The 1-additive fuzzy measure, can be defined using only values for singletons as:
The 2-additive fuzzy measure, can be defined only its values for singletons and pairs as:
Definition 8
(Aggregation operator—Agg, Beliakov et al. 2007) An n-argument aggregation operator is mapping \( Agg:\left[ {0, 1} \right]^{n} \to \left[ {0,1} \right] \) with the following properties:
-
1.
\( {\text{if}} x_{i} \le x_{j } {\text{for all}} i \in 1, \ldots , n, {\text{then}} Agg\left( {x_{1} , \ldots , x_{n} } \right) \le Agg\left( {y_{1} , \ldots , y_{n} } \right) \),
-
2.
$$ Agg\left( {1, \ldots , 1} \right) = 1, $$
-
3.
$$ Agg\left( {0, \ldots , 0} \right) = 0. $$
Definition 9
(Ordered Weighted Mean—OWA, Yager 1988) An OWA aggregation operator is a mapping OWA: [0.1]n → [0. 1] such that:
where weights \( w_{i} \in \left[ {0, 1} \right]\, {\text{for}}\, i = 1, \ldots , n, \mathop \sum \limits_{i = 1}^{n} w_{i} = 1 \,{\text{and }}\,x_{\left( i \right)} \) indicates that the indices have been permuted so that \( 0 \le x_{\left( 1 \right)} \le \ldots \le x_{\left( n \right)} \le 1. \)
Composite Maintenance Sustainability Index
According to Nooteboom (2007), ‘system has a sustainable development if that development enables it to maintain its wholeness as an integral system, whilst also maintaining its role as part of a larger system on which it depends’. Considering the above and the definition of sustainable production presented by Moldavska and Velo (2017), maintenance as a subsystem of the production system is sustainable if it contributes to the sustainability of the large system (of which it is an element) while maintaining its own sustainability. This definition brings three important implication for the design of a maintenance assessment model. Firstly, evaluation of results of maintenance system in relation to the superior system represented by, for example, stakeholders and their requirements. Secondly, the assessment of operations and resources of the maintenance system (capacity of maintenance). Thirdly, the ability to conduct a comprehensive analysis of not only relationships and dependencies occurring within the maintenance system, but also relations between maintenance and its environment. In general, the model for sustainable maintenance assessment (Jasiulewicz-Kaczmarek and Żywica 2018):
-
(a)
should integrate three factors of sustainability (economic, environmental and social);
-
(b)
should take into account links between maintenance and its stakeholders (maintenance system is an open system, the improvement of maintenance processes cannot be carried out in isolation from its stakeholders, i.e. other organizational units of the enterprise that affect maintenance system and are affected by it in the same time);
-
(c)
should be based both on financial and non-financial measures (for business managers, financial aspects of maintenance activities are generally important, hence they most often emphasize the importance of financial criteria, while other organizational units of the enterprise formulate their criteria referring to the broadly understood quality of maintenance activities);
-
(d)
should be easy to interpret (the assessment result should be shown in an aggregated form, while allowing decomposition to lower levels, showing decision makers the impact of each criterion on the final result and indicating potential directions for improvement).
In order to fulfil assumption (a)—(c) given above, Kaplan-Norton Balanced Scorecard (BSC) model was used. Since the BSC was introduced, many authors have proposed modifications for adapting the initial BSC to other models that are specific to different areas or industrial environments (Figge et al. 2002; Sari et al. 2015; Singh et al. 2018). To assess the maintenance sustainability the original Kaplan-Norton BSC model was modified and new structure of the model was developed. This new one includes four perspectives: financial (FP), maintenance stakeholders (MS), and maintenance processes (MP), innovation and development (ID). These perspectives are then divided into particular criteria (Fig. 3). The assessment criteria and detailed issues for each of the criteria were distinguished based on literature analysis and were consulted with experts (researchers and practitioners from enterprises) in order to assess the completeness of the criteria, their scope, as well as usefulness and possibility of using of the model in real business. The detailed description of the perspectives and respective criteria can be found in (Jasiulewicz-Kaczmarek and Żywica 2018).
Assumption (d) concerns the method of presentation of the result of the assessment. This result is to be presented in the form of an interpretation-friendly composite index, which will allow determining the impact (importance) of each perspective and the criteria describing it on the aggregate assessment result. According to Gan et al. (2017), weighting and aggregation of index components are critically important steps in any sustainability assessment. The weights of criteria reflect the relative importance of different criteria in the sustainability performance of a system, while aggregation essentially reflects the substitutability of different dimensions. In general, the properties of an aggregate function can be related to mathematical properties and behavioural properties (mathematical properties point to a formally correct aggregation of criteria, while behavioural properties express relationships between criteria). In order to aggregate perspectives and criteria that are dependent on one another, a non-additive fuzzy integral was applied. Fuzzy integral allows considering human’s subjective perception and uncertainty. Moreover, it encompasses the inter-dependency between criteria, which is a very important issue regarding sustainability assessment. Fuzzy measure used in the model is non-additive, which means that the importance of all features combined does not have to be equal to the total importance of individual features. In order to model the interactions, the CMSI model uses Choquet integral. The main steps of constructing a CMSI can be described as follow (Fig. 4):
-
Step 1. Determination the importance of decision perspective/criteria with linguistic variables
The first step in developing a maintenance sustainability index focuses on weighting individual elements (perspectives and criteria). The determination of the importance of the evaluated perspectives and criteria is carried out by a team of experts. Since the step is carried out by a team of experts and because of their subjectivity and cognitive differences, linguistic variables are used and then aggregated by fuzzy arithmetic. The Fuzzy Number Ordered Weighted Average (FN-OWA) operator was used in the model for averaging expert evaluations, which is an OWA operator, designed especially for fuzzy numbers and linguistic data (Chen and Chen 2003). The main reason why FN-OWA was chosen is that it has the ability to aggregate not only quantitative data, but also can handle linguistic as well as crisp data. Moreover, it is an idempotent operator, which means that an operator retains the same linguistic state as if all input criteria had equal values (Sadiq and Tesfamariam 2008). Aggregated fuzzy weights are then de-fuzzified in order to be applied in constructing fuzzy measure.
-
Step 2. Construction of fuzzy measure
One important issue in sustainable assessment is the need to express not only the importance of individual features but also interactions between them. There are three kind of interactions: synergy, inhibitory and non-interaction. The classic probability theory only uses the third one, and thus is unrealistic in this case. Fuzzy measure can be applied to all three situations. It represents the importance of a criterion in the set of criteria and can be considered as generalization of probability measure. In order to lower the number of coefficients (which increases exponentially with number of perspectives/criteria) and satisfy the monotonicity and continuity, CMSI model uses λ-measure (see Jasiulewicz-Kaczmarek and Żywica (2018)). There are normally three kinds of interactions between two criteria A and B (µ denotes importance/weight): synergetic interaction, which can be represented by µ (A ∪ B) > µ(A) + µ(B); inhibitory interaction, which can be represented by µ(A ∪ B) < µ(A) + µ(B); non-interaction, which can be represented by µ(A ∪ B) = µ(A) + µ(B).
One of the problems that can occur in the case of expert assessments is the situation in which individual criteria will be rated so high (close to 1) that pairs, triples etc. of criteria, due to the monotonicity of the fuzzy measure, will have very similar values (effectively equal to 1). While in the case of aggregation using a weighted average such a situation is not a problem, in the case of a fuzzy measure and the Choquet integral it can lead to undesirable results (shallowing/equalization of criteria weights and total omission of interactions among criteria). To significantly reduce the impact of these problems on the aggregation result, the q-measure proposed by Mohamed and Xiao (2003) was applied in CMSI model. q-measure is an extension of λ-measure that simplifies its computations and allows for choosing the λ parameter. The applied algorithm finds such a re-scaling of the data that models best the interactions between the criteria.
-
Step 3. Calculate the aggregate value (CMSI)
The purpose of aggregation functions is to combine multiple numerical inputs, into a single numerical value, which in some sense represents all the inputs. Many aggregation functions have a limitation mainly from their natural assumption that input criteria are independent of each other (Beliakov and Wu 2019). This is not always true in reality, where the independence of criteria cannot be assumed. Some interaction among different criteria does exist, including the independence, the complement, and the correlation (Grabisch and Roubens 2000). To take all of the interaction among the attributes into account, it has been proposed to use the fuzzy measure in the calculation of the overall aggregation result (Grabisch and Roubens 2000). The fuzzy integral is used in the sustainable maintenance assessment to combine assessments since it does not require criteria to be independent. Thanks to stability of Choquet integral under positive linear transformations, the exact numerical scale in relation to which the calculations are made is not relevant. This way, collecting data from experts is way simplified, and it allows assessment with use of linguistic scale.
To apply the model, we need to present it to the decision-makers in order to collect data. The assessment team from the factory assess the issues describing individual criteria in a numerical scale (maturity matrix). The assessments are then aggregated using the model. CMSI measures the organization’s maintenance sustainability in range [0; 1]. The value of CMSI closer to ‘0’ indicates that the maintenance is un-sustainable; whereas a value closer to ‘1’ means that, the maintenance structure is sustainable and contributes to the sustainability of the manufacturing system. The calculated CMSI value can be then used to determinate the relative importance between perspectives and criteria. This way the CMSI can stand as help for decision-makers by directing their attention to the areas that need improving.
Extension of CMSI model for decision support system
Goals
The model presented above (Chapter ‘Composite Maintenance Sustainability Index’) cannot by easy used in the decision support systems, expert systems or in any automated decision tools. In particular, after analysing the original CMSI model in terms of use as decision support system two potential problems were noted:
-
1.
How to fine-tune the model for the needs of a given enterprise, based on detailed data obtained from a small group of experts? The first important requirement for decision support system is the ability to adapt it to the characteristics of a given company (industry and character of realized processes). If we want to make binding decisions based on the indicator, it must be possible to tune some of its aspects. Such a possibility will certainly also increase the confidence of current experts in the system.
-
2.
The key question when analysing any model is which criteria limit the entire model, i.e. even a small decrease in their value will significantly affect the entire result. Similarly, it is important to determine the criteria that should be improved in in the first place, so that the index value will increase to the greatest extent. The main task of the decision support system is to identify attributes from both groups based on the current values. In addition, it is necessary to be able to quantify to what extent the change in a given criterion will an affect the final index value. As a result, it will be possible to simulate potential future values and choose an improvement strategy that will maximize growth while minimizing the cost and workload.
Design principles of an extended model
Sometimes, instead of building a new model, a much better approach is to extend existing model with what is lacking in it, i.e. higher-order interactions. In this way, the structure of the original model would be preserved, at the same time enriching and adapting it. Following subsection extends the original CMSI model to address the aforementioned problems (Subsection: Goals). All extensions are presented on the top layer of CMSI model (perspectives layer). Similar extensions have been applied at the criteria level.
Model fine-tuning
To solve this problem a universal method is proposed. Implementation details depend largely on what goal one want to achieve. We will modify the fuzzy measure of CMSI using some results on representation of k-additive fuzzy measures obtained by Grabisch (1997). Moreover, new knowledge from experts will be represented by means of interaction indexes. The method involves decomposition of original fuzzy measure of CMSI model into interaction coefficients and then combining them with new expert data, (any order interactions). The proposed method consist of following steps:
-
1.
Decompose the original fuzzy measure \( \mu_{orig} \) to interaction indexes ICMSI using (7). Select the interactions that will be used as a basis for new measure \( {\mathcal{T}}_{orig} \subset 2^{x} \).
-
2.
Prepare new expert data as interactions for some subset of criteria \( A \in {\mathcal{T}}_{orig} \subset 2^{x} \) denoted as \( I_{new} \left( A \right) \).
-
3.
Build new interaction indexes based on selected interactions.
$$ I^{\alpha } \left( K \right) = I_{M}^{\alpha } \left( K \right) = \left\{ {\begin{array}{*{20}l} {\frac{{I_{\text{orig}} \left( K \right) + \alpha MI_{\text{new}} \left( K \right)}}{1 + \alpha M}} \hfill & {K \in {\mathcal{T}}_{\text{orig}} \backslash {\mathcal{T}}_{\text{new}} } \hfill \\ {I_{\text{orig}} \left( K \right) } \hfill & {K \in {\mathcal{T}}_{\text{orig}} \backslash {\mathcal{T}}_{\text{new}} ,} \hfill \\ {\alpha MI_{\text{new}} \left( K \right)} \hfill & {K \in {\mathcal{T}}_{\text{new}} \backslash {\mathcal{T}}_{\text{orig}} } \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$(12)where \( \alpha \in \left[ {0, 1} \right] \) denotes the weight (importance) of new expert data and
$$ M = \sup \left\{ {m:I_{m}^{1}\, {\text{generates proper fuzzy measure}}} \right\}. $$(13) -
4.
Define new fuzzy measure using
$$ \mu_{\alpha } \left( A \right) = \mathop \sum \limits_{T \subset A} \mathop \sum \limits_{k = 0}^{\left| X \right| - \left| T \right|} \alpha_{k} \mathop \sum \limits_{{\begin{array}{*{20}c} {K \subset X\backslash T} \\ {\left| K \right| = k} \\ \end{array} }} I^{\alpha } \left( {K \cup T} \right), $$(14)where
$$ \alpha_{k} = - \mathop \sum \limits_{l = 0}^{k - 1} \frac{{\alpha_{l} }}{k - l + 1}\left( {\begin{array}{*{20}c} k \\ l \\ \end{array} } \right). $$(15)
The method has its advantages and disadvantages. It is general in the sense that it can be applied to any fuzzy measure (not only λ-measure) without losing any information. The resulting fuzzy measure will be k-additive (depending on original and new expert data) and it is possible to make only slight changes to original model. On the other hand, this approach is complex (both conceptually and computationally) which may lead to some difficulties.
In the following example a special case of this method was propose. We take only Shapley values from original measure (step 1) and then add second order interactions based on new expert data (step 2). This approach is more suitable for extension of λ-measure, since it allows avoiding addition of superficial data (high order interactions from λ-measure) into new model. The resulting fuzzy measure will be 2-additive, which in practice means the construction of a completely new model. On the other hand, it allows to significantly reducing the complexity of the method.
Description of the usage of proposed method in the case of CMSI is presented below. λ-measure can be uniquely defined by only first level interactions (Shapley values). Therefore, it is reasonable to select only these interactions as the basis for the new fuzzy measure. In addition, we obtain estimates about the second-level interactions (between pairs of criteria) from the experts. This approach is also justified, as experts are usually able to answer the question whether the interaction between the two criteria occurs and what is its nature (positive or negative). Opinions across many experts may be then averaged.
In this case new interaction index will be defined
From this, it can be observed that new fuzzy measure will be 2-additive so we can simplify the formula for M (Grabisch 1997):
Finally, fuzzy measure can be defined as
For α = 0 we obtain additive fuzzy measure which is similar to original CMSI model. For any \( \alpha \in \left( {0, 1} \right] \) new model is 2-additive.
Limiting by the least grown criteria
Although this behaviour is not noticeable in the original CMSI model, the problem turns out to be relatively simple to solve. The OWA operator is known for an effective mechanism limiting the impact of extreme values on the final value of aggregation. In addition, OWA is a special case of Choquet’s integral, which makes it a very good candidate to extend the original model. Let \( \mu_{OWA} \) be the fuzzy measure of the OWA operator expressed as Choquet integral and \( \mu_{CMSI} \) denotes original fuzzy measure of CMSI model. Those two fuzzy measures can be combined using nearly any aggregation operator Agg
Observation of the results leads to the conclusion that using geometrical mean as Agg gives very good results. The new measure combines the features of both measures, allowing the model to be limited by less parametrized criteria, while maintaining the distribution of weights given by experts in the original CMSI. Of course, the behaviour of the new measure depends largely on the choice of OWA operator weights. Weights cannot be too drastic, because in this way we can disrupt the original model. On the other hand, it is necessary to increase significantly the weight of the weakest criteria. A number approaches have been suggested for obtaining the weights (Filev and Yager 1994, 1998; Fuller 2007; Grabisch 2011; Beliakov and Wu 2019). Based on our numerical experiments we recommend one of those two formulas to obtain OWA weights:
In this decision support system, the first formula was used which resulted in the following OWA weight vector (0.1; 0.2; 0.3; 0.4).
Proposed criteria evaluation method
To determine the impact of given criterion on the value of the entire model, partial derivatives of the CMSI model was used.
Definition 10
The partial derivative of the CMSI model C(x) with respect to the criterion c denoted as \( \delta_{{C_{i} }} \) is defined as:
The use of a simple and well-known tool to analyse the impact of individual criteria on the model has many advantages. First, the calculation of the partial derivative for each criterion is not very computationally demanding. One can also assume with great certainty that the target recipients of the decision support system know the derivative concept and its interpretation. This will make it much easier to convince them to use the system, as back box tools are often reluctantly received by practitioners. Moreover, thanks to the fusion of the fuzzy measure with the OWA operator and the transfer of interaction coefficients from a small group of experts, the partial derivative very well reflects the decision space. It gives a good picture of which criteria are important while hiding unnecessary complexity.
Figure 5 presents the behaviour of three variants of CMSI model. It can be easily seen that model based on weighted mean is too simple to be applied in decision support system. Its derivative is constant; hence, system will give constant recommendation regarding further improvement. Original CMSI model offers much more diverse derivative, but still its actual values are very similar to weighted mean. In this extended CMSI model one can observe that derivative is the smaller the higher the value of given criterion.
Of course, the model could be analysed in a different way. For example, using a rule-based system, in which experts would determine in what conditions specific decisions, should be taken. Unfortunately, the number of criteria in the model is so large that such a tool would require at least several hundred rules. The rule base could be built to some extent automatically using machine-learning techniques, but unfortunately, there is not enough data. In addition, it is not possible to obtain a large amount of such data due to the high cost of accurately determining the CMSI value and its analysis, which is actually performed quarterly or even annually. Another solution would be to apply the Shapley value and the interaction index described in the original paper (Jasiulewicz-Kaczmarek and Żywica 2018). These, however, remain constant regardless of the current value of individual criteria (they depend only on the fuzzy measure). This only allows to define a very general characteristics of the model, showing which criteria are the most important in the general case. However, this is not enough to support decisions effectively.
Evaluation of the proposed model
Structure and development of decision support system
To evaluate the proposed model the decision support system (DSS) was performed. The underlying CMSI model has been expanded using data from an external enterprise to fit its industry specificities. The extension used second-order interaction factors, which were then combined with the original CMSI fuzzy measure (Jasiulewicz-Kaczmarek Żywica 2018) according to the proposed method. The developed DSS was performed using R software (version 3.4.4) (R Core Team 2014) and was deployed to shinyapps.io cloud hosting platform (https://bikol.shinyapps.io/URApp). The logical structure of decision support system was presented in Fig. 6b.
The developed decision support system (Fig. 7) supplies recommendations for the decision maker by suggesting which perspectives (divided into particular criteria) should be developed in the first place, in order to improve the CMSI (and thus the overall sustainable maintenance performance) in the optimal way. System provides information in both numerical and visual form, which makes it easy to interpret and apply in real situations.
Numerical experiments and discussion
The proposed decision support systems, except of showing a calculated value of CMSI, provides the decision maker with two types of additional information:
-
The derivative calculated based on considered criterion—the higher the derivative, the higher the influence of this criterion on the CMSI.
-
The percent—the difference (in percent), between the CMSI calculated with given criterion with current value and value 0.
At the beginning, two hypothetical cases were analysed to illustrate the functioning of the developed DSS. In the first one, all the criteria have a value of 0.3. The obtained derivatives, percentages and CMSI index for such a situation are presented in Table 1.
It can be easily noticed that assigning 0.3 to all criteria results in CMSI of value 0.3, which is the index showing that sustainable maintenance practices are at very low level at analysed situation.
In the second case, financial perspective criteria (f1—maintenance stakeholders costs; f2—maintenance costs) and innovation and development criteria (id1—competence of maintenance workers; id2—maintenance infrastructure; id3—satisfaction of maintenance workers) have been severely increased and are of equal value = 0.7. Remaining perspectives parameters—i.e. maintenance stakeholders criteria (s1—production and quality, s2—safety and health, s3—environment, s4—communication and cooperation with stakeholders) and maintenance process criteria (p1—analysis and environment; p2—execution and measurement, p3—planning and scheduling maintenance processes; p4—management of external services; p5—management of spare parts and consumables) are still of equal value = 0.3. The obtained results for such initial parameters are presented in Table 2.
Analysis of the obtained results let to notice that improving two elements of the maintenance function: (1) financial and (2) innovation and development have positive impact and allows to increase the final level of sustainability. In particular, the CMSI value equals 0.451 what means that the sustainable maintenance level equals 45, 1%. However it is worth to emphasize that provided improvements in FP and ID areas and more than 100% increase of initial values in each of the criterions allows to obtain the CMSI value on the level 0.453 what means it increase of about 50%. Moreover, it must be emphasized that in real industrial environment it is practically impossible to obtain such huge improvements on such a large set of parameters in one planning period.
Therefore, to illustrate the practical value of the developed model let us analyse a real industrial case. Let assume that the medium size company from plastic industry wants to improve sustainability results in maintenance area. In order to determine the level of effectiveness of the applied practices in relation to the economic environmental and social requirements of sustainable development in the enterprise, an assessment was carried out and the value of the CMSI index was calculated. The initial parameters defined during the provided surveys have been presented in Table 3. The initial result of CMSI parameter equals exactly 0.411 (Fig. 8) what means that company’s policy lies below the middle between sustainable and unsustainable maintenance, and thus allows for future improvements in perspectives describes by distinguished criteria.
Following the level of distinguished parameters decision-makers, in 2 years period (including two one-year decision periods) decided to improve the level of sustainable maintenance by putting more pressure on Maintenance Process (MP). In particular, two criteria were the object of improvements: p1 (analysis and improvement) and p2 (execution and measurement). The decision of improving these two criteria was caused by the lowest value of initial parameters for these factors (marked with red colour). Therefore necessary activities (such as: application of formal methods and techniques of data analysis, collecting and analysing data on future investments in machinery and equipment, efficiency planning, identification of OSH and environmental hazards during the implementation of unscheduled services, etc.) were realized. It allowed increasing both of analysed parameters by 0.1 in each year. Finally, after the second year of provided improvements the final CMSI index increased to 0.442. Detailed information about obtained parameters after each year of realized improving activities are presented in Table 4.
Let us analyse, how should be provided improvements when we used a proposed DSS model. The most important index that must be firstly taken into account before taking the decision is “Derivative” index. The high value of this index means that the specific parameter will have the high importance for the CMSI index (what means the sustainable manufacturing level). When analyse the derivatives for the initial parameters of the company we can observe that the highest values are for the criteria f1 (1.615) and f2 (1.430). Therefore, to increase the sustainable manufacturing index the necessary activities should be attended.
Let us imagine that in the first year the company will make necessary improvements in this year (e.g. by reduction costs of losses related to production stoppages resulting from breakdowns, reduction costs connected with potentially accidental events and accidents of maintenance workers, operators and third parties during maintenance works, additional finance for training costs for employees, etc.) and increase both of this parameters by 0.1. The provided analysis (see the middle part of Table 5) shows that it will allow to obtain the CMSI index of 0.435 (what means the increase of 0.024 when compare with the beginning level of the CMSI index and increase of 0.007 when compare with improvements already done by the company).
When analysing the situation at the end of the first year of improvements we can see that the criteria with the highest derivative index have changed. In this case, the highest derivatives have two criteria: s2 (1.421) and id2 (1.412). This means that additional activities should be done to improve these areas of maintenance in the company. If the company will be able to increase these criteria by 0.1 each the CMSI index will additionally increase and will equal 0.453 (see the bottom part of Table 5).
When we compare results obtained by the company (Table 4) and obtained following the suggestions of DSS system (Table 5) we can easily notice that the final value of CMSI index is better for the second situation. While the result obtained by the company (CMSI index) increased by seven, 54%, the improvements which are the result of suggestions given by the DSS allowed to increase value of CMSI index by more than 10%. It proves the efficiency of the proposed model and its practical value for industrial purposes.
Conclusions
The main purpose of this article was to develop a non-aggregate method of combining various decision indicators representing the criteria for a balanced assessment of the maintenance system, into a new synthetic indicator that would allow identifying weak points and pointing out potential directions of improvement actions.
By analysing any multi-criteria system assessment model (the subject of the study was a maintenance assessment model from the perspective of sustainable production requirements), in which the assessment result is presented in the form of a composite index (aggregate value), decision-makers generally ask themselves two questions: (1) Which of the assessment criteria limit the whole model, i.e. even a slight decrease in their value will significantly affect the whole result?; (2) Which criteria should be developed first so that the index value increases the most?
To solve these problems the article proposed a new method of the indicator merge. Interactions between input data play a key role in this method. Compared with the classic aggregation of indicator values, the proposed solution has several advantages. First, it allows looking at the process of combining indicators from a different perspective, i.e. through interactions between criteria. This approach to the problem allows the identification of cooperating and mutually exclusive attributes, and thus a better fit to the data. In addition, it is much easier to understand and interpret the indicator obtained using this representation. Thanks to implementing the approach presented in the article, it is possible to extend the existing maintenance assessment model with new properties while maintaining its original character.
To justify effectiveness of proposed approach, it was applied to the actual CMSI indicator, which was therefore generalized and expanded, so that it could be used in decision support system to help decision-makers in improving economic, social and environmental results of maintenance system. The case study presented in the paper show the real benefit of using the proposed approach to analysing the actual results of maintenance system from sustainability point of view and forecasting future actions.
Based on the findings of this research, future studies could focus on building a fuzzy measure in an interaction-based approach. Another area of further research is to determine to what extent the indicators combined by combining fuzzy measures differ from the indicators obtained by standard aggregation of their values.
Abbreviations
- BSC:
-
Balance Scorecard
- CMSI:
-
Composite Maintenance Sustainability Index
- GRI:
-
Global Reporting Initiatives
- ISM:
-
Interpretive Structural Modelling
- KPI:
-
Key Performance Indicator
- OEE:
-
Overall Equipment Efficiency
- TBL:
-
Triple Bottom Line
- MICMAC:
-
Matriced’ Impacts Croisés Appliquée á un Classement
- TOPSIS:
-
Technique for Order Preference by Similarity to an Ideal Solution
References
Ajukumar, V. N., & Gandhi, O. P. (2013). Evaluation of green maintenance initiatives in design and development of mechanical systems using an integrated approach. Journal of Cleaner Production, 51, 34–46.
Amrina, E., & Yulianto, A. (2018). Interpretive structural model of key performance indicators for sustainable maintenance evaluatian in rubber industry. IOP Conference Series: Materials Science and Engineering, 319(1), 012055.
Beliakov, G., Pradera, A., Calvo, T. (2007). Aggregation functions: a guide for practitioners, Studies in Fuzziness and Soft Computing 221. Springer.
Beliakov, G., & Wu, J.-Z. (2019). Learning fuzzy measures from data: simplifications and optimization strategies. Information Sciences, 494, 100–113.
Bevilacqua, M., Bottani, E., Ciarapica, F. E., Costantino, F., Di Donato, L., Ferraro, A., et al. (2020). Digital twin reference model development to prevent operators’ risk in process plants. Sustainability, 12, 1088.
Bilge, P., Emec, S., Seliger, G., & Jawahir, I. S. (2017). Mapping and integrating value creation factors with life-cycle stages for sustainable manufacturing. Procedia CIRP, 61, 28–33.
Bokrantz, J., Skoogh, A., Berlin, C., & Stahre, J. (2017). Maintenance in digitalised manufacturing: Delphi-based scenarios for 2030. International Journal of Production Economics, 191, 154–169.
Bokrantz, J., Skoogh, A., Berlin, C., Wuest, T., & Stahre, J. (2019). Smart maintenance: An empirically grounded conceptualization. International Journal of Production Economics, 223, 107534. https://doi.org/10.1016/j.ijpe.2019.107534.
Boral, S., Chaturvedi, S. K., Naikan, V. N. A., & Howard, I. M. A. (2019). Hybrid AI based conceptual decision making model for sustainable maintenance strategy selection. In Y. Morteza, C. Shankar, P. Dilbagh, B. Siddhartha, & P. Chatterjee (Eds.), Advanced multi-criteria decision making for addressing complex sustainability issues (pp. 63–90). Pennsylvania: IGI Global.
Chen, S. J., & Chen, S. M. (2003). A new method for handling multi-criteria fuzzy decision making problems using FN-IOWA operators. Cybernetics and Systems, 34, 109–137.
Chen, J., Zhang, R., & Wu, D. (2018). Equipment maintenance business model innovation for sustainable competitive advantage in the digitalization context: Connotation, types, and measuring. Sustainability, 10, 3970.
Choquet, G. (1954). Theory of capacities. Annales de l’institut Fourier, 5, 131–295.
Costantino, F., Di Gravio, G., & Tronci, M. (2013). Integrating environmental assessment of failure modes in maintenance planning of production systems. Applied Mechanics and Materials, 295–298, 651–660.
EN 13306:2017 Maintenance—Maintenance terminology.
Figge, F., Hahn, T., Schaltegger, S., & Wagner, M. (2002). The sustainability balanced scorecard–linking sustainability management to business strategy. Business Strategy and the Environment, 11(5), 269–284.
Filev, D., & Yager, R. R. (1994). Learning OWA operator weights from data. In Proceedings of 1994 IEEE 3rd International Fuzzy Systems Conference, Orlando, FL, (vol. 1, pp. 468–473).
Filev, D., & Yager, R. R. (1998). On the issue of obtaining OWA operator weights. Fuzzy Sets and Systems, 94, 157–169.
Flammer, C. (2013). Corporate social responsibility and shareholder reaction: The environmental awareness of investors. Academy of Management Journal, 56(3), 758–781.
Franciosi, C., Di Pasquale, V., Iannone, R., & Miranda, S. (2020a). Multi-stakeholder perspectives on indicators for sustainable maintenance performance in production contexts: An exploratory study. Journal of Quality in Maintenance Engineering. https://doi.org/10.1108/JQME-03-2019-0033.
Franciosi, C., Iung, B., Miranda, S., & Riemma, S. (2018). Maintenance for sustainability in the Industry 4.0 context: A scoping literature review. IFAC PapersOnLine, 51–11, 903–908.
Franciosi, C., Lambiase, A., & Miranda, S. (2017). Sustainable maintenance: A periodic preventive maintenance model with sustainable spare parts management. IFAC PapersOnLine, 50–1, 13692–13697.
Franciosi, C., Voisin, A., Miranda, S., Riemma, S., & Iung, B. (2020b). Measuring maintenance impacts on sustainability of manufacturing industries: From a systematic literature review to a framework proposal. Journal of Cleaner Production, 260, 121065.
Fraser, K., Hvolby, H. H., & Tseng, T. L. (2015). Maintenance management models: A study of the published literature to identify empirical evidence. International Journal of Quality & Reliability Management, 32(6), 635–664.
Fuller, R. (2007). On obtaining OWA operator weights: a short survey of recent developments. In Proceedings of 5th IEEE International Conference Computing Cybernetics, (pp. 241–244). Gammarth, Tunisia.
Gan, X., Fernandez, I. C., Guo, J., Wilson, M., Zhao, Y., Zhou, B., et al. (2017). When to use what: Methods for weighting and aggregating sustainability indicators. Ecological Indicators, 81, 491–502.
Grabisch, M. (1997). K-order additive discrete fuzzy measures and their representation. Fuzzy Sets and Systems, 92, 167–189.
Grabisch, M. (2011). OWA Operators and nonadditive integrals In: R.R. Yager et al. (Eds.) Recent developments in the OWA operators, STUDFUZZ, (vol. 265, pp. 3–15).
Grabisch, M., & Roubens, M. (2000). Application of the Choquet integral in multicriteria decision making. In M. Grabisch, T. Murofushi, & M. Sugeno (Eds.), Fuzzy Measures and Integrals—Theory and Applications (pp. 348–374). Berlin: Physica Verlag.
ITA. (2007). How does commerce define sustainable manufacturing? US Department of Commerce (USDOC), International Trade Administration. Retrieved 17 Dec 2020 from, http://www.trade.gov/competitiveness/sustainablemanufacturing/how_doc_defines_SM.asp.
Iung, B., & Levrat, E. (2014). Advanced maintenance services for promoting sustainability. Procedia CIRP, 22, 15–22.
Jasiulewicz-Kaczmarek, M. (2013). Sustainability: orientation in maintenance management - theoretical background. In P. Golinska, et al. (Eds.), Eco-Production and Logistics. Emerging Trends and Business Practices (pp. 117–134). Berlin: Springer.
Jasiulewicz-Kaczmarek, M. (2019). Sustainable maintenance assessment model of enterprise technical infrastructure. Poznan: Poznan University of Technology Publishers.
Jasiulewicz-Kaczmarek, M., & Gola, A. (2019). Maintenance 4.0 technologies for sustainable manufacturing—An overview. IFAC PapersOnLine, 52–10, 91–96.
Jasiulewicz-Kaczmarek, M., & Żywica, P. (2018). The concept of maintenance sustainability performance assessment by integrating balanced scorecard with non-additive fuzzy integral. Eksploatacja i Niezawodnosc—Maintenance and Reliability, 20, 650–661.
Kannegiesser, M., & Günther, H. O. (2014). Sustainable development of global supply chains—Part 1: Sustainability optimization framework. Flexible Services and Manufacturing Journal, 26(1–2), 24–47.
Li, H., Mi, S., Li, Q., Wen, X., Qiao, D., & Luo, G. (2020). A scheduling optimization method for maintenance, repair and operations service resources of complex products. Journal of Intelligent Manufacturing, 31, 1673–1691.
Macchi, M., Roda, I., Negri, E., & Fumagalli, L. (2018). Exploring the role of Digital Twin for asset lifecycle management. FAC PapersOnLine, 51–11, 790–795.
Machado, C. G., Winroth, M. P., & da Silva, E. H. D. R. (2020). Sustainable manufacturing in Industry 40: an emerging research agenda. International Journal of Production Research, 58(1), 1462–1484.
Maletič, D., Maletič, M., Al-Najjar, B., & Gomišček, B. (2018). Development of a model linking physical asset management to sustainability performance: an empirical research. Sustainability, 10(12), 4759.
Marquez, A. C. (2007). The maintenance management Framework. Models and methods for complex systems maintenance. London: Springer.
Meng, K., Qian, X., Lou, P., & Zhang, J. (2020). Smart recovery decision-making of used industrial equipment for sustainable manufacturing: Belt lifter case study. Journal of Intelligent Manufacturing, 31, 183–197.
Mohamed, M. A., & Xiao, W. (2003). Q-measures: An efficient extension of the Sugeno lambda-measure. IEEE Transactions on Fuzzy Systems, 11(3), 419–426.
Moldavska, A., & Velo, T. (2017). The concept of sustainable manufacturing and its definitions: A content analysis-based literature review. Journal of Cleaner Production, 166(10), 744–755.
Moldavska, A., & Velo, T. (2019). A holistic approach to corporate sustainability assessment: Incorporating sustainable development goals into sustainable manufacturing performance evaluation. Journal of Manufacturing Systems, 50, 53–68.
Murofushi, T. (1992). Techniques for reading fuzzy measures (I). The Shapley value with respect to a fuzzy measure. In 2nd Fuzzy Workshop, (pp. 39–48). Nagaoka, Japan.
Murofushi, T., Soneda, S. (1993). Techniques for reading fuzzy measures (III). Interaction index. In 9th Fuzzy System Symposium (pp. 693–696). Sapporo, Japan.
Nooteboom, S. (2007). Impact assessment procedures for sustainable development: A complexity theory perspective. Environmental Impact Assessment Review, 27(7), 645–665.
Pires, S., Sénéchal, O., Loures, E., & Jimenez, J. (2016). An approach to the prioritization of sustainable maintenance drivers in the TBL framework. IFAC-PapersOnLine, 49, 150–155.
R Core Team (2014). R: A language and Environment for Statistical Computing. R Foundation for Statistical Computing Vienna, Austria. http://www.R-project.org.
Raouf, A. (2009). Maintenance quality and environmental performance improvement: An integrated approach. In M. Ben-Daya, et al. (Eds.), Handbook of maintenance management and engineering (pp. 649–664). London: Springer.
Sadiq, R., & Tesfamariam, S. (2008). Developing environmental indices using fuzzy numbers ordered weighted averaging (FN-OWA) operators. Stochastic Environmental Research and Risk Assessment, 22(1), 494–505.
Sari, E., Shaharou, A., Maaram, A., & Yazid, A. M. (2015). Sustainable maintenance performance measures: A pilot survey in Malaysian automotive companies. Procedia CIRP, 26, 443–448.
Satolo, E. G., Simon, A. T., & Braga, S. S. (2016). Sustainable development and the integration of normative standards. In R. Dubey & A. Gunasekaran (Eds.), Strategic Management of Sustainable Manufacturing Operations (pp. 192–226). Pennsylvania: IGI Global.
Savino, M. M., Macchi, M., & Mazza, A. (2015). Investigating the impact of social sustainability within maintenance operations: An action research in heavy industry. Journal of Quality in Maintenance Engineering, 21(3), 310–331.
Seliger, G., Kim, H.-J., Kernbaum, S., & Zettl, M. (2008). Approaches to sustainable manufacturing. International Journal of Sustainable Manufacturing, 1(1/2), 58–77.
Sénéchal, O. (2018). Performance indicators nomenclatures for decision making in sustainable conditions based maintenance. IFAC PapersOnLine, 51–11, 1137–1142.
Sénéchal, O., & Trentesaux, D. (2019). A framework to help decision makers to be environmentally aware during the maintenance of cyber physical systems. Environmental Impact Assessment Review, 77, 11–22.
Shin, S.-J., Kim, D. B., Shao, G., Brodsky, A., & Lechevalier, D. (2017). Developing a decision support system for improving sustainability performance of manufacturing processes. Journal of Intelligent Manufacturing, 28, 1421–1440.
Singh, R. K., & Gupta, A. (2020). Framework for sustainable maintenance system: ISM–fuzzy MICMAC and TOPSIS approach. Annals of Operations Research, 290, 643–676.
Singh, S., Olugu, E. U., Musa, S. N., & Mahat, A. B. (2018). Fuzzy-based sustainability evaluation method for manufacturing SMEs using balanced scorecard framework. Journal of Intelligent Manufacturing, 29, 1–18.
Sugeno, M. (1974). Theory of Fuzzy Integrals and Its Applications. Ph.D. thesis Tokyo Institute of Technology.
Takata, S., Kimura, F., van Houten, F. J. A. M., Westkämper, E., Shpitalni, M., Ceglarek, D., et al. (2004). Maintenance: Changing role in life cycle management. Annals of the CIRP, 53(2), 643–656.
Turner, C. J., Emmanouilidis, C., Tomiyama, T., Tiwari, A., & Roy, R. (2019). Intelligent decision support for maintenance: An overview and future trends. International Journal of Computer Integrated Manufacturing, 32(10), 936–959.
Wang, J., Xu, S. X., & Xu, G. (2020). Intelligent decision making for service and manufacturing industries. Journal of Intelligent Manufacturing, 31, 2089–2090.
Wu, H. Y., Chen, J. K., & Chen, I. S. (2012). Performance evaluation of aircraft maintenance staff using a fuzzy MCDM approach. International Journal of Innovative Computing, Information and Control, 8(6), 3919–3937.
Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Transactions on Systems, Man and Cybernetics, 18, 183–190.
Acknowledgements
The project/research was financed in the framework of the project Lublin University of Technology-Regional Excellence Initiative, funded by the Polish Ministry of Science and Higher Education (Contract No. 030/RID/2018/19).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jasiulewicz-Kaczmarek, M., Żywica, P. & Gola, A. Fuzzy set theory driven maintenance sustainability performance assessment model: a multiple criteria approach. J Intell Manuf 32, 1497–1515 (2021). https://doi.org/10.1007/s10845-020-01734-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-020-01734-3