Hybrid post-quantum Transport Layer Security formal analysis in Maude-NPA and its parallel version
Author and article information
Abstract
This article presents a security formal analysis of the hybrid post-quantum Transport Layer Security (TLS) protocol, a quantum-resistant version of the TLS protocol proposed by Amazon Web Services as a precaution in dealing with future attacks from quantum computers. In addition to a classical key exchange algorithm, the proposed protocol uses a post-quantum key encapsulation mechanism, which is believed invulnerable under quantum computers, so the protocol’s key negotiation is called the hybrid key exchange scheme. One of our assumptions about the intruder’s capabilities is that the intruder is able to break the security of the classical key exchange algorithm by utilizing the power of large quantum computers. For the formal analysis, we use Maude-NPA and a parallel version of Maude-NPA (called Par-Maude-NPA) to conduct experiments. The security properties under analysis are (1) the secrecy property of the shared secret key established between two honest principals with the classical key exchange algorithm, (2) a similar secrecy property but with the post-quantum key encapsulation mechanism, and (3) the authentication property. Given the time limit T = 1,722 h (72 days), Par-Maude-NPA found a counterexample of (1) at depth 12 in T, while Maude-NPA did not find it in T. At the same time T, Par-Maude-NPA did not find any counterexamples of (2) and (3) up to depths 12 and 18, respectively, and neither did Maude-NPA. Therefore, the protocol does not enjoy (1), while it enjoys (2) and (3) up to depths 12 and 18, respectively. Subsequently, the secrecy property of the master secret holds for the protocol up to depth 12.
Cite this as
2023. Hybrid post-quantum Transport Layer Security formal analysis in Maude-NPA and its parallel version. PeerJ Computer Science 9:e1556 https://doi.org/10.7717/peerj-cs.1556Main article text
Introduction
As an early precaution in dealing with future attacks from quantum computers, extensive research efforts have been spent to construct post-quantum cryptographic protocols, replacing classical cryptographic protocols. This has been motivated by the fact that most of the asymmetric cryptosystems used today will be no longer secure under large-scale quantum computers. The reason is that the computationally hard mathematical problems on which these cryptosystems are relying can be efficiently solved by a sufficiently large quantum computer even though they are intractable for conventional computers. For instance, the integer factorization problem is no longer hard under a large-scale quantum computer running Shor’s algorithm (Shor, 1994). In recent years, with the involvement of many giants, such as Intel, IBM, and Google, different and stronger quantum computers have been introduced, making a practical one closer to reality. That motivates many cryptography and security research groups to investigate on building new post-quantum cryptographic protocols as well as analyzing their security.
In 2019, the Amazon Web Services (AWS) team proposed a quantum-resistant version of the Transport Layer Security (TLS) 1.2 protocol (Rescorla & Dierks, 2008), namely the hybrid post-quantum TLS Protocol (Campagna & Crockett, 2021), where TLS is known as one of the most important cryptographic protocols, protecting numerous communications over the Internet every day. Two parallel key exchange schemes are employed in the proposed protocol, namely a classical key exchange algorithm and a post-quantum key encapsulation mechanism (KEM), which is the reason why the word “hybrid” is used in its name. In the proposal, the classical key exchange algorithm is fixed as Elliptic Curve Diffie-Hellman (ECDH), while the post-quantum KEM (PQ KEM) can be, for example, Kyber (Bos et al., 2018) (precisely CRYSTALS-Kyber) and BIKE (Aragon et al., 2019). That hybrid scheme is expected to make a negotiated secret key at least as secure as ECDH against a classical attacker and at least as secure as the selected PQ KEM against a quantum attacker.
Our previous work (Tran et al., 2022) presented the Maude-NPA formal specification of the hybrid post-quantum TLS protocol, where Maude-NPA (Escobar, Meadows & Meseguer, 2006) is a powerful tool for analyzing cryptographic protocols. Maude-NPA is implemented in Maude (Durán et al., 2020), a specification/programming language based on rewriting logic, and supports an unbounded number of session executions as well as protocol participants. For modeling intruders’ capabilities, the tool uses the Dolev-Yao intruder model (Dolev & Yao, 1983) and the strand model (Thayer, Herzog & Guttman, 1998). In this manner, the intruder is given the capability of fully controlling the network, for example, intercepting & modifying messages and impersonating some protocol participants to send some messages to other participants. Maude-NPA is based on narrowing and backward search. Narrowing is a generalization of term rewriting that allows variables in subject terms and replaces pattern matching by unification. The backward search starts from a given insecure pattern, i.e., an attack pattern, representing insecure states, and runs backwardly to check whether it is reachable from an initial state. If an initial state is found, the attack concerned is a valid attack on the protocol; otherwise, the protocol is secure against the attack. Several optimization techniques to reduce the search space have been developed (see the article by Escobar, Meadows & Meseguer (2008)).
This article presents a formal analysis of the hybrid post-quantum TLS protocol with Maude-NPA. This is an extended version of our previous work (Tran et al., 2022), which provided a first attempt at formally specifying the protocol in Maude-NPA. The analysis belongs to the symbolic approach, which is typically preferred by formal method researchers. Whereas, its complementary, namely the computational approach, is often used by cryptographers. A computational proof gives a tighter security guarantee because it takes probability and complexity into account, but it is not easy to understand for non-experts in cryptography, and hard to mechanize the proof. A symbolic verification is easier to understand, computer-verified, and suitable for automation, but it often needs to make some idealizing assumptions. We conduct the formal analysis with not only Maude-NPA but also a parallel version of Maude-NPA (called Par-Maude-NPA for short) (Do et al., 2022) to make the best use of multicore architectures.
In summary, our contributions in this work include the Maude-NPA formal specification of the Hybrid PQ TLS and the formal analysis of three security properties:
-
The secrecy property of the ECDH shared secret key established between two honest principals. Par-Maude-NPA found a counterexample of this property at depth 12 in the time T = 1722 h (72 days), while Maude-NPA did not find it in T.
-
The secrecy property of the PQ KEM shared secret key established between two honest principals. As the same time T, Par-Maude-NPA did not find any counterexample of this property up to depth 12, and neither did Maude-NPA up to depth 10.
-
The authentication property, which states that if client A has completed the handshake, apparently with server B, then B is the actual principal who has communicated with A. As the same time T, Par-Maude-NPA did not find any counterexample up to depth 18, and neither did Maude-NPA up to depth 17.
The analysis results confirm that the protocol enjoys (2) and (3) up to depths 12 and 18, respectively, while it does not enjoy (1). Subsequently, the secrecy property of the master secret holds for the protocol up to depth 12. By using Par-Maude-NPA, we achieve a better running performance than the original tool in terms of analysis time. Hybrid PQ TLS is one large case study formalized in Maude-NPA. Through this work, we also would like to show a case in which Par-Maude-NPA is capable of detecting an attack, while Maude-NPA fails to do so due to an excessively long analysis time, which has not been demonstrated in Do et al. (2022). The complete protocol specification and the attack patterns reported in this article can be found at https://doi.org/10.5281/zenodo.7919153.
In the remainings, we give some preliminaries related to Maude-NPA and Maude in Section ‘Preliminaries’. We describe the exchange messages in the Hybrid PQ TLS protocol in Section ‘Hybrid Post-Quantum TLS 1.2’ and the Maude-NPA formal specification of the protocol in Section ‘Protocol formal specification in Maude-NPA’. Afterward, Section ‘Analysis experiments’ reports the results of the experiments we have conducted with Maude-NPA and Par-Maude-NPA. Finally, Section ‘Related work’ mentions some related case studies and Section ‘Conclusion’ summarizes our article.
Preliminaries
Maude-NPA (Escobar, Meadows & Meseguer, 2006) is implemented in Maude (Durán et al., 2020), a declarative language and high-performance rewriting logic tool for specifying, programming, and verifying programs/systems, especially concurrent programs/systems. Maude supports both order-sorted equational logic and rewriting logic (Meseguer, 2010). Several formal analysis facilities, such as reachability analysis and LTL model checking, are implemented in Maude, making it possible to specify and analyze complex systems. This section briefly introduces the syntax of the Maude language (see the article by Durán et al. (2020) and the book by Clavel et al. (2007) for more details), how narrowing works, and how Par-Maude-NPA was parallelized.
Functional modules
A functional module M specifies an order-sorted equational logic theory (Σ, E) with the syntax:
fmod
is
endfm -
importations of previously defined modules (
… orprotecting
… orextending
…)including -
sorts and subsorts (
ssort
or.
s s′sorts
or.
ssubsort
s′<
). -
function symbols (
fop
s1 … sn → s [att1 … attk]:
). -
variables (
v v′vars
).
where s and s′ are sort names; v and v′ are variable names; and att1, …, attk are equational attributes, such as
assoc
comm E may contain a collection of equations, which may be either unconditional (
eq
=
.
ceq
=
if
.
= System modules
A system module R specifies a rewrite theory (Σ, E, R) with the syntax:
mod
is
endm
rl [
]
:
=>
.
crl [
]
:
=>
if
.
=> Narrowing
Narrowing is a generalization of term rewriting that allows logical variables in terms and replaces pattern matching by unification. To describe how narrowing works, in the following, we use a classical example in the Maude book (Clavel et al., 2007). The following system module specifies a concurrent machine to buy cakes (
c
a
q
buy-c
buy-a
change
mod NARROWING-VENDING-MACHINE is
sorts Coin Item Marking Money State .
subsort Coin < Money .
op empty : -> Money .
op __ : Money Money -> Money [assoc comm id: empty] .
subsort Money Item < Marking .
op __ : Marking Marking -> Marking [assoc comm id: empty] .
op <_> : Marking -> State .
ops $ q : -> Coin .
ops c a : -> Item .
var M : Marking .
rl [buy-a] : < M $ > => < M a q > [narrowing] .
rl [buy-c] : < M $ > => < M c > [narrowing] .
eq [change] : q q q q M = $ M [variant] .
endm
<_>
__
empty
narrowing
variant
< M1 >
Money
< M1 >
< M1 > ⇝σ1, buy-a < a q M2 >
< M1 > ⇝σ′
1, buy-c < c M2’ >
M2
M2’
Money
M1
M2, M ↦→ M2 and σ′1 = M1 ↦→ M2’
M
M2’
buy-a
buy-c
M
< a q M2 >
< M1 > ⇝σ1, buy-a < a q M2 > ⇝σ2, buy-c < a c q M3 > ⇝σ3, buy-a < a a c q M4 >
M3
M4
Money
{M2 ↦→ M3, M ↦→ a q M3} and σ3 = { M3 ↦→ q q q M4, M ↦→ a c M4} with
the rewrite rules buy-c and buy-a, respectively. In the third nar-
rowing step, when we apply the substitution σ3, the two obtained in-
stances of < a c q M3 > and the left-hand side of the rewrite rule buy-a
are < a c q q q q M4 > and < a c M4 >
change
buy-a
< a a c q M4 >
State Par-Maude-NPA
Par-Maude-NPA (Do et al., 2022) has been developed in order to improve the running performance of Maude-NPA by the parallel mechanism. Maude-NPA basically uses a breadth-first search (BFS) to explore the state space backwardly from a given insecure attack pattern. Given a set of states in layer l, for each state in the set, the backward narrowing can be performed independently to obtain its successor states in layer l + 1. Par-Maude-NPA makes use of this point to parallelize the backward narrowing tasks for states at the same layer, so that successor states are generated in parallel at each layer. Generally speaking, the breadth-first search in Maude-NPA is transformed into a parallel breadth-first search in Par-Maude-NPA without altering the number or form of the states in the state space. Par-Maude-NPA uses a master-worker model with one master and multiple workers, where the master distributes (or assigns) jobs to each worker in a well-balanced way. The tool uses a shared cache maintained by the master and a local cache maintained by each worker to avoid making unnecessary duplications of jobs.
Hybrid Post-Quantum TLS 1.2
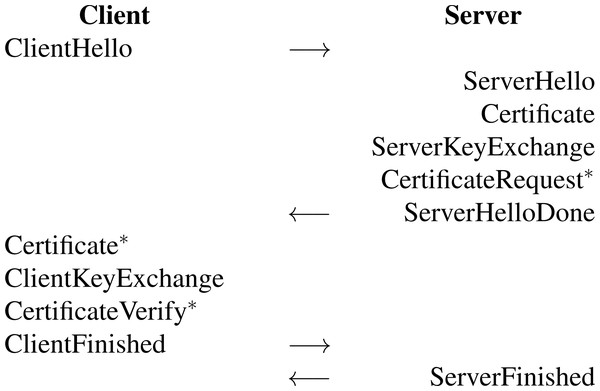
Figure 1 depicts the exchanged messages in a full handshake of the Hybrid PQ TLS protocol. In this figure, ∗ indicates that the message is not sent unless client authentication is requested. The hybrid key exchange mechanism in the proposed protocol directly impacts on ClientHello, ServerHello, ServerKeyExchange, and ClientKeyExchange messages.
Let C and S denote a client and a server, respectively. When C wants to start a new session with S, C starts by sending a ClientHello message to S. This message in the full handshake mode consists of the protocol version, a random number, an empty session ID, a list of cipher suites (cryptographic algorithms supported by C) in order of C’s preference, and a set of post-quantum KEM parameters (including both the name of KEM and its parameters) supported by C. When receiving the ClientHello message, S responds to C with a ServerHello message, containing the protocol version, a random number, a non-empty session ID, and a selected cipher suite. S then sends his/her digital certificate (via a Certificate message) and a ServerKeyExchange message to C. The ServerKeyExchange message includes the ECDH & KEM public keys and a signature over the two public keys together with the two random numbers previously sent in the Hello messages (i.e., ClientHello and ServerHello messages) signed by S’s long-term private key. In the case when client authentication is requested, which is optional, a CertificateRequest message will also be sent. S then sends a ServerHelloDone message to C, informing the completion of the hello phase on the server side.
Figure 1: Messages exchanged in a full handshake of the hybrid post-quantum TLS protocol (Campagna & Crockett, 2021).
An asterisk (∗) indicates that the message is not sent unless client authentication is requested.When receiving the ServerHelloDone message, C replies to S with a ClientKeyExchange message, consisting of the client’s ECDH public key and the KEM ciphertext (generated by the algorithm
Encaps When receiving the ClientFinished message, S validates it and sends a ServerFinished message. Once C receives the ServerFinished message, it also has to validate that the message is correct. After that, both sides can securely exchange messages by encrypting them under the negotiated handshake key.
Protocol formal specification in Maude-NPA
Through this section, we present how we formally specify the Hybrid PQ TLS protocol in Maude-NPA. Before going into detail about the protocol formal specification, we first describe the strand notation through a running example to see how strands can be used to model the protocol execution.
Formal specification by strands
Maude-NPA uses strands (Thayer, Herzog & Guttman, 1998) to specify the execution of the protocol under analysis as well as the capabilities of the intruder. Each strand is a sequence of positive and negative messages and possibly with some unique fresh data as follows: ::r1,…,rk::[+(msg1),−(msg2),…,−(msgi)|+(msgi+1),…]
where r1, …, rk denote unique fresh data consumed by the principal performing the strand (they would be, for example, secret keys, unique random numbers, and session identifiers). A positive message +(msg) and a negative message −(msg) denote sending and receiving the message msg, respectively. The vertical bar is used to distinguish between present and future when the strand appears in a state description. Messages appearing before the bar were sent/received in the past, while messages appearing after the bar will be sent/received in the future. Let us consider a classical security protocol, namely Needham-Schroeder-Lowe Public Key (NSLPK) protocol (Lowe, 1995), to illustrate how strands would be used to specify the protocol execution. The protocol consists of the following three exchange messages:
-
P → Q:pk(Q, P; NP)
-
Q → P:pk(P, NP; NQ; Q)
-
P → Q:pk(Q, NQ)
where P and Q denote two principal identifiers, NP and NQ are nonces (unguessable values) generated by P and Q, respectively, and pk(P, m) denotes the encryption of message m by the public key of P. The three messages exchanged can be explained as follows. P first generates a nonce NP and sends it together with P’s identifiers encrypted by Q’s public key to Q. Upon receiving that message, Q decrypts it and obtains a nonce. Q generates a new nonce NQ, encrypts the nonce received, the new nonce, and Q’s identifiers under P’s public key, and sends the result back to P. Upon receiving the response message, P decrypts it, checking if one of the nonces is exactly the one that P has sent before in the first message. If that is the case, P responds to Q with the other nonce encrypted under Q’s public key.
Maude-NPA provides some built-in sorts, such as the sort
Msg
Fresh
Name
Nonce
Msg
sorts Name Nonce .
subsort Name Nonce < Msg . The nonce constructor is specified by the following operator:
op n : Name Fresh -> Nonce [frozen] .
frozen
P
r
Name
Fresh
n(P,r)
P
r
op pk : Name Msg -> Msg [frozen] .
Q
N
Name
Nonce
:: r ::
[ nil | +(pk(Q, P ; n(P,r))), -(pk(P, n(P,r) ; N ; Q)), +(pk(Q, N)), nil ] The strand says that initially, given a unique fresh
r
P
n(P,r)
Q
P
Q
P
n(P,r)
N
Q
P
P
Q
N
Q
:: r::
r
;
op _;_ : Msg Msg -> Msg [frozen] . In the same manner, the strand that describes how the protocol is executed from the Q side can be specified as follows:
:: r ::
[ nil | -(pk(Q, P ; N)), +(pk(P, N ; n(Q,r) ; Q)), -(pk(Q, n(Q,r))), nil ] Strands are also used for the specification of the intruder capabilities. But in this case, such an intruder strand is limited to be in the form of a sequence of negative messages (possibly empty) followed by one positive message combining all previous variables under a function symbol. For example, the intruder’s capability in encrypting any message by any public key is specified as follows:
:: nil :: [ nil | -(M), +pk(P,M), nil ]
M
Msg
M
P Protocol formal specification
This section describes the Maude-NPA formal specification of the Hybrid PS TLS protocol. We start with the definition of KEMs and how to model them in Maude-NPA.
KEM specification
A key encapsulation mechanism is a tuple of algorithms (
KeyGen
Encaps
Decaps -
() →(pk, sk): A probabilistic key generation algorithm, which generates a public & secret key pair pk & sk.KeyGen -
(pk) →(c, k): A probabilistic encapsulation algorithm, which takes as input a public key pk and generates an encapsulation (or ciphertext) c and a shared key k∈K.Encaps -
(c, sk) →k: A deterministic decapsulation algorithm, which takes as inputs a ciphertext c and a secret key sk, and returns as output a shared key k∈K.Decaps
A KEM is ϵ- correct if for all (pk, sk)←
KeyGen
Encaps
Decaps Intuitively, ϵ is the probability such that
Decaps
Encaps
Decaps
Decaps
Decaps To model KEMs in Maude-NPA, we first introduce sorts
PqSk
PqPk
Cipher
PqKey
op pqSk : Name Fresh -> PqSk [frozen] .
Fresh
Name
Decaps
op decap : Cipher PqSk -> PqKey [frozen] .
Decaps
KeyGen
Encaps
PqSk
Encaps
encapCipher
encapKey
op pqPk : PqSk -> PqPk [frozen] .
op encapCipher : PqPk PqSk -> Cipher [frozen] .
op encapKey : PqPk PqSk -> PqKey [frozen] .
KeyGen
Encaps
op $pqKey : PqSk PqSk -> PqKey [frozen] .
eq encapKey(pqPk(S:PqSk), S2:PqSk) = $pqKey(S:PqSk, S2:PqSk) [variant] .
eq decap(encapCipher(pqPk(S:PqSk),S2:PqSk), S:PqSk)
= $pqKey(S:PqSk, S2:PqSk) [variant] .
variant
$pqKey
encapKey
decap
Encaps
Decaps
Decaps
Encaps ECDH and key calculation specification
To model ECDH in Maude-NPA, we first introduce the following sorts:
sort Scalar Point ECKey .
subsort Point < ECKey .
Point
Scalar
ECKey
op p : -> Point .
op scl : Name Fresh -> Scalar [frozen] .
op gen : Point Scalar -> Point [frozen] .
op _*_ : Scalar Scalar -> Scalar [frozen assoc comm] .
p
scl
gen
assoc
comm
eq gen(gen(P:Point, S:Scalar), S2:Scalar)
= gen(P:Point, S:Scalar * S2:Scalar) [variant] .
PreMasterSecret
MasterSecret
op pms : ECKey PqKey -> PreMasterSecret [frozen] .
op ms : PreMasterSecret Rand Rand Point Cipher -> MasterSecret [frozen] .
Rand Honest principal specification
rd
sess
cert
sig
enc
op rd : Name Fresh -> Rand [frozen] .
op sess : Name Fresh -> Session [frozen] .
op cert : Name -> Cert [frozen] .
op sig : Name Msg -> Msg [frozen] .
op enc : MasterSecret Msg -> Msg [frozen] .
S
M
MS
enc(MS,M)
M
MS
sig(S,M)
M
S
sig(priKey(S),M)
cert(S)
S
S
r1
r2
r3
Fresh
C
S
Name
N
SS
Rand
Session
PK1
PK2
Point
PqPk
:: r1,r2,r3 ::
[ nil |
+(ch ; rd(C,r1)),
-(sh ; N ; SS),
-(sc ; cert(S)),
-(ske ; PK1 ; PK2 ; sig(S, PK1 ; PK2 ; rd(C,r1) ; N)),
+(cke ; gen(p,scl(C,r2)) ; encapCipher(PK2, pqSk(C,r3))),
+(cf ; enc(ms(pms(gen(PK1,scl(C,r2)), encapKey(PK2, pqSk(C,r3))),
rd(C,r1), N, gen(p,scl(C,r2)), encapCipher(PK2, pqSk(C,r3))),
(ch ; rd(C,r1)) ++
(sh ; N ; SS) ++
(sc ; cert(S)) ++
(ske ; PK1 ; PK2 ; sig(S, PK1 ; PK2 ; rd(C,r1) ; N)) ++
(cke ; gen(p,scl(C,r2)) ; encapCipher(PK2, pqSk(C,r3))))
),
nil ]
ch
sh
sc
ske
cke
cf
Msg
++
C
S
rd(C,r1)
PK1
PK2
PK2
++
++
++
(sh ; N ; SS) ++ (sc ; cert(S))
(sh ; N ; SS ; sc ; cert(S))
++ In the same manner, we specify the protocol execution from a server’s side. The strand below specifies the server execution up to the ClientFinished message:
:: r1,r2,r3,r4 ::
[ nil |
-(ch ; N),
+(sh ; rd(S,r1) ; sess(S,r2)),
+(sc ; cert(S)),
+(ske ; gen(p,scl(S,r3)) ; pqPk(pqSk(S,r4)) ;
sig(S, gen(p,scl(S,r3)) ; pqPk(pqSk(S,r4)) ; N ; rd(S,r1))),
-(cke ; PK1 ; CP),
-(cf ; enc(ms(pms(gen(PK1,scl(S,r3)), decap(CP, pqSk(S,r4))),
N, rd(S,r1), PK1, CP),
(ch ; N) ++
(sh ; rd(S,r1) ; sess(S,r2)) ++
(sc ; cert(S)) ++
(ske ; gen(p,scl(S,r3)) ; pqPk(pqSk(S,r4)) ;
sig(S, gen(p,scl(S,r3)) ; pqPk(pqSk(S,r4)) ; N ; rd(S,r1))) ++
(cke ; PK1 ; CP))
),
nil ]
CP
Cipher Intruder capabilities
Maude-NPA uses the standard Dolev-Yao intruder model (Dolev & Yao, 1983). The intruder is given the capability of fully controlling the network, in particular, the intruder can intercept and learn information from any message in the network; fake and synthesize messages based on the gleaned information; and impersonate some principal to send the faking message to some other. Let
X
Y
Msg
:: nil :: [ nil | -(X), -(Y), +(X ; Y), nil ] &
:: nil :: [ nil | -(X ; Y), +(X), nil ] &
:: nil :: [ nil | -(X ; Y), +(Y), nil ] & The intruder may consume a fresh to generate by themself a random number and a scalar serving as an ECDH secret key, which is specified as follows:
:: r :: [ nil | +(rd(i,r)), nil ] &
:: r :: [ nil | +(scl(i,r)), nil ] &
i With KEMs, if the intruder has learned some public key
PK2
SK
CP
:: nil :: [ nil | -(PK2), -(SK), +(encapCipher(PK2,SK)), nil ] &
:: nil :: [ nil | -(PK2), -(SK), +(encapKey(PK2,SK)), nil ] &
:: nil :: [ nil | -(CP), -(SK), +(decap(CP,SK)), nil ] & With ECDH, an important assumption we suppose is that the intruder can break the key exchange security by utilizing the power of quantum computation. That is, if the intruder knows the two ECDH public keys exchanged between a client and a server, then the intruder can derive the shared secret key. This capability is specified by the following strand:
:: nil :: [ nil | -(gen(p,S)), -(gen(p,S2)), +(gen(p,S * S2)), nil ]
S
S2
Scalar The complete specification of the intruder capabilities includes some more strands, which are omitted showing here. Again, readers can find them at https://doi.org/10.5281/zenodo.7919153.
Checking the specification
To increase trust in the correctness of what has been formally specified, a state pattern is defined proving that it is possible to successfully complete a protocol handshake between two principals. This must be fulfilled, otherwise, the analysis coming later would be meaningless. Let
c
s
Name
ATTACK-STATE
eq ATTACK-STATE(10) =
:: r1,r2,r3 ::
[ nil,
+(ch ; rd(c,r1)),
-(sh ; N ; SS),
-(sc ; cert(s)),
-(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)),
+(cke ; gen(p, scl(c,r2)) ; encapCipher(PK2, pqSk(c,r3))),
+(cf ; enc(ms(pms(gen(PK1, scl(c,r2)), encapKey(PK2, pqSk(c,r3))),
rd(c,r1), N, gen(p, scl(c,r2)), encapCipher(PK2, pqSk(c,r3))),
(ch ; rd(c,r1)) ++
(sh ; N ; SS) ++
(sc ; cert(s)) ++
(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)) ++
(cke ; gen(p, scl(c,r2)) ; encapCipher(PK2, pqSk(c,r3))))),
-(sf ; ... )
| nil ]
|| empty
|| nil || nil || nil
[nonexec] .
10
ATTACK-STATE(10)
...
Msg
nil
c
s Analysis experiments
Three experiments analyze the following three properties for the protocol with each of Maude-NPA and Par-Maude-NPA: (1) the secrecy property of the ECDH shared secret key established between two honest principals, (2) the secrecy property of the PQ KEM shared secret key established between two honest principals, and (3) the authentication property, i.e., if A has completed the protocol execution apparently with B, then B is indeed the principal who has communicated with A.
Secrecy property of ECDH shared secret key
The first property we would like to check is whether the intruder can glean the ECDH shared secret key when a client and a server have completed the handshake. To check that property, we specify another Maude-NPA attack pattern, i.e.,
ATTACK-STATE(0)
ATTACK-STATE(10)
empty
gen(PK1, scl(c,r2)) inI, empty
PK1
c
s
scl(c,r2)
_inI
_!inI
PK1
gen(p, scl(c,r2))
gen(PK1, scl(s,r2)) We have checked the attack pattern with both the original Maude-NPA and Par-Maude-NPA. Par-Maude-NPA found a counterexample for the attack pattern in about 1,722 h (nearly 72 days), meaning that the intruder can learn the ECDH shared secret key established between the honest client and the honest server. That counterexample state contains four sections: (1) state ID, (2) set of current protocol and intruder strands, (3) intruder knowledge, and (4) sequence of messages. To understand how the attack can happen, we show (4)—the message sequence leading to the counterexample as follows:
1 +(ch ; rd(c,#3:Fresh)),
2 -(ch ; rd(c,#3:Fresh)),
3 +(sh ; rd(s,#4:Fresh) ; sess(s,#6:Fresh)),
4 +(sc ; cert(s)),
5 +(ske ; gen(p, scl(s,#0:Fresh)) ; pqPk(pqSk(s,#2:Fresh)) ;
sig(s, gen(p, scl(s,#0:Fresh)) ; pqPk(pqSk(s,#2:Fresh)) ;
rd(c,#3:Fresh) ; rd(s,#4:Fresh))),
6 -(ske ; ...),
7 +(gen(p, scl(s,#0:Fresh)) ; pqPk(pqSk(s,#2:Fresh)) ;
sig(s, gen(p, scl(s,#0:Fresh)) ; pqPk(pqSk(s,#2:Fresh)) ;
rd(c,#3:Fresh) ; rd(s,#4:Fresh))),
8 -(sh ; rd(s,#4:Fresh) ; sess(s,#6:Fresh)),
9 -(sc ; cert(s)),
10 -(ske ; ...),
11 +(cke ; gen(p, scl(c,#1:Fresh)) ;
encapCipher(pqPk(pqSk(s,#2:Fresh)), pqSk(c,#5:Fresh))),
12 -(cke ; ...),
13 +(gen(p, scl(c,#1:Fresh)) ;
encapCipher(pqPk(pqSk(s,#2:Fresh)),pqSk(c,#5:Fresh))),
14 -(gen(p, scl(c,#1:Fresh)) ;
encapCipher(pqPk(pqSk(s,#2:Fresh)),pqSk(c,#5:Fresh))),
15 +(gen(p, scl(c,#1:Fresh))),
16 -(gen(p, scl(s,#0:Fresh)) ;
pqPk(pqSk(s,#2:Fresh)) ; sig(s, gen(p, scl(s,#0:Fresh)) ;
pqPk(pqSk(s,#2:Fresh)) ; rd(c,#3:Fresh) ; rd(s,#4:Fresh))),
17 +(gen(p, scl(s,#0:Fresh))),
18 -(gen(p, scl(s,#0:Fresh))),
19 -(gen(p, scl(c,#1:Fresh))),
20 +(gen(p, scl(s,#0:Fresh) * scl(c,#1:Fresh))),
21 +(cf ; ...),
22 -(cke ; gen(p, scl(c,#1:Fresh)) ;
encapCipher(pqPk(pqSk(s,#2:Fresh)), pqSk(c,#5:Fresh))),
23 -(cf ; ...),
24 +(sf ; ...),
25 -(sf ; ...) We insert line numbers on the left side for easy reference in the following explanation. Client
c
s
#3:Fresh
s
c
gen(p, scl(s,#0:Fresh))
...
c
s
c
s
gen(p, scl(s,#1:Fresh))
:: nil :: [ nil | -(gen(p,S)), -(gen(p,S2)), +(gen(p,S * S2)), nil ] the intruder learns the ECDH shared secret between
c
s
c
s
s
c The counterexample was found by Par-Maude-NPA at depth 12. It means that the found state is located at depth 12 from the root of the backward reachability tree constructed by the tool. In this tree, the root is the attack pattern, and a child node is connected to its parent node by an action of an honest principal or the intruder. With Maude-NPA, it did not find the counterexample in the same amount of time T. The detail of the experimental results is discussed in Section ‘Experimental results’.
Secrecy property of PQ KEM shared secret key
ATTACK-STATE(1)
ATTACK-STATE(0)
ATTACK-STATE(1)
ATTACK-STATE(10)
encapKey(PK2, pqSk(c,r3)) inI, empty
ATTACK-STATE(1)
PK2
encapCipher(PK2, pqSk(c,r3))
encapKey(PK2, pqSk(c,r3)) Par-Maude-NPA did not find any counterexample up to depth 12, confirming that the intruder cannot learn the PQ KEM shared secret established between the client and the server up to the bounded depth. Together with the previous analysis experiment, it follows that even though the intruder can learn the ECDH shared secret, the intruder cannot learn the master secret. We leave a detailed discussion about the analysis result in Section ‘Experimental results’.
Authentication property
The next property we would like to check is the authentication property, i.e., if client A has completed the handshake apparently with server B, then B is indeed the principal who has communicated with A. We define the following
ATTACK-STATE(2)
eq ATTACK-STATE(2) =
:: r1,r2,r3 ::
[ nil,
+(ch ; rd(c,r1)),
-(sh ; N ; SS),
-(sc ; cert(s)),
-(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)),
+(cke ; gen(p,pt(c,r2)) ; encapCipher(PK2, pqSk(c,r3))),
+(cf ; enc(ms(pms(gen(PK1, pt(c,r2)), encapKey(PK2, pqSk(c,r3))),
rd(c,r1),N,gen(p,pt(c,r2)),encapCipher(PK2, pqSk(c,r3))),
(ch ; rd(c,r1)) ++
(sh ; N ; SS) ++
(sc ; cert(s)) ++
(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)) ++
(cke ; gen(p,pt(c,r2)) ; encapCipher(PK2, pqSk(c,r3))))),
-(sf ; ... )
| nil ]
|| empty
|| nil
|| nil
|| never(
:: r’,r1’,r2’,r3’ ::
[ nil |
-(ch ; rd(c,r1)),
+(sh ; N ; SS),
+(sc ; cert(s)),
+(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)),
-(cke ; gen(p,pt(c,r2)) ; encapCipher(PK2, pqSk(c,r3))),
-(cf ; enc(ms(pms(gen(PK1,pt(c,r2)), encapKey(PK2, pqSk(c,r3))),
rd(c,r1),N,gen(p,pt(c,r2)),encapCipher(PK2, pqSk(c,r3))),
(ch ; rd(c,r1)) ++
(sh ; N ; SS) ++
(sc ; cert(s)) ++
(ske ; PK1 ; PK2 ; sig(s, PK1 ; PK2 ; rd(c,r1) ; N)) ++
(cke ; gen(p,pt(c,r2)) ; encapCipher(PK2, pqSk(c,r3))))),
+(sf ; ... ),
nil ]
& STR:StrandSet
|| IK:IntruderKnowledge)
[nonexec] .
...
Msg
empty
never
c
s
s
c
s
c
never Experimental results
We have conducted experiments for the three above-mentioned attack patterns with Maude-NPA and Par-Maude-NPA on a supercomputer that carries 1.5 TB of memory and four 2.8 GHz microprocessors, where each microprocessor has 16 cores. Because we were only able to use one such supercomputer for our experiments and could have predicted that it would take a long time to complete each of the total six experiments, we started the six experiments on the supercomputer simultaneously. With Par-Maude-NPA, we used one master and eight workers with at most 256 GB of memory and 16 microprocessor cores for each experiment. With Maude-NPA, at most 256 GB of memory and 4 microprocessor cores were used for each experiment. This resource allocation is reasonably fair because of 1.5 TB memory (=6 × 256 GB memory) and 4 × 16 cores (>3 × 16 cores + 3 × 4 cores), although the OS uses some resources, which should be negligible. Note that Maude-NPA uses one core for each experiment and the six experiments may use a total of about 1.5 TB of memory for about 1,722 h. Table 1 shows the experimental results for the three attack patterns with Maude-NPA and Par-Maude-NPA. The first column denotes the attack number corresponding to each attack pattern. The next three columns denote the running time, the depth at which Maude-NPA reaches, and the result of each analysis, respectively, with Maude-NPA and similarly for Par-Maude-NPA with the last three columns. In the Result column, the symbol ∅ denotes no counterexample is found up to a bounded depth; while the symbol × denotes a counterexample is found and the protocol is insecure against the attack. In the Depth column, “H x” denotes the analysis is still running at depth x and has not been completed, where “H” stands for “Handling”. On the other hand, “F x” denotes the analysis is completed at depth x, where “F” stands for “Finished”.
| Attack number | Maude-NPA | Par-Maude-NPA | ||||
|---|---|---|---|---|---|---|
| Time (h:m:s) | Depth | Result | Time (h:m:s) | Depth | Result | |
| 0 | 1,722:20:23 | H 11 | ∅ | 1,722:20:23 | F 12 | × |
| 1 | 1,722:20:23 | H 11 | ∅ | 1,722:20:23 | H 13 | ∅ |
| 2 | 1,722:20:23 | H 18 | ∅ | 1,722:20:23 | H 19 | ∅ |
With attack pattern number 0, as T = 1,722 h, 20 min, and 23 s (nearly 72 days), Par-Maude-NPA completed the analysis at depth 12 and found a counterexample. We decided to stop all of the six experiments as the time T because the long time had been spent. We report the results of the five other experiments as the same time T. Also with attack pattern number 0, as the same time T, Maude-NPA only reached depth 11 and was handling it. Therefore, no counterexample was found by Maude-NPA in T.
With attack pattern number 1, as the same time T, both Par-Maude-NPA and Maude-NPA did not find any counterexample. Par-Maude-NPA and Maude-NPA were handling depth 13 and depth 11, respectively. Observing the number of reachable states at each depth, we see that it is increased after each layer depth. The number of reachable states at each depth of the three analysis experiments is depicted in Table 2, where the hyphen symbol denotes the data is not available because the analysis with that given attack is not conducted at that given depth. Note that the data shown in Table 2 are exactly the same up to depths 10, 10, and 17 for the three attack patterns 0, 1, and 2, respectively, with Maude-NPA and Par-Maude-NPA.
| Depth | Attack 0 | Attack 1 | Attack 2 |
|---|---|---|---|
| 1 | 15 | 15 | 8 |
| 2 | 30 | 30 | 5 |
| 3 | 51 | 56 | 2 |
| 4 | 86 | 101 | 2 |
| 5 | 150 | 165 | 2 |
| 6 | 261 | 262 | 2 |
| 7 | 435 | 408 | 2 |
| 8 | 695 | 610 | 2 |
| 9 | 1,067 | 871 | 2 |
| 10 | 1,597 | 1,216 | 4 |
| 11 | 2,374 | 1,757 | 7 |
| 12 | 3,679 | 2,634 | 10 |
| 13 | – | – | 19 |
| 14 | – | – | 40 |
| 15 | – | – | 95 |
| 16 | – | – | 246 |
| 17 | – | – | 602 |
| 18 | – | – | 1,355 |
With attack pattern number 2, similarly, both Par-Maude-NPA and Maude-NPA did not find any counterexample, and were handling at depth 19 and depth 18, respectively, in the time T. The number of reachable states at each depth from 1 to 13 is reasonably small. However, it quickly increases at the deeper depths, especially depths 17 and 18. Therefore, we guess that the experiments would not converge at depth 19 or a bit deeper depth.
The six experiments show that using Par-Maude-NPA helped us to significantly reduce the analysis time in this Hybrid PQ TLS case study. To measure precisely how much Par-Maude-NPA is faster than Maude-NPA, we conduct some more experiments with attack number 0, bounded depths 8 and 9, numbers of workers 8, 12, and 16, and show the results in Table 3. For example, when the bounded depth is 8, we can increase the running performance of Maude-NPA with Par-Maude-NPA as 3.8x, 4.2x, and 4.6x faster than that with Maude-NPA, respectively. The improvement of the running performance of Maude-NPA with Par-Maude-NPA for the bounded depth 9 is better than that for the bounded depth 8 in this case study. That is because the number of states at the bounded depth 9 is larger than that at the bounded depth 8. It says that the more states located at a depth, the more improvement will be obtained by using Par-Maude-NPA. Indeed, the number of states at deeper depths (see Table 2) increases quickly, and then the use of Par-Maude-NPA will achieve a better improvement compared to Maude-NPA in terms of running performance, which was partially shown in these experiments and also in the six experiments described above.
| Attack | Bounded | Maude-NPA | Par-Maude-NPA | Improvement | |
|---|---|---|---|---|---|
| number | depth | Time (h:m:s) | #workers | Time (h:m:s) | (how faster) |
| 0 | 8 | 70:39:03 | 8 | 18:46:37 | 3.8x |
| 12 | 16:54:15 | 4.2x | |||
| 16 | 15:26:02 | 4.6x | |||
| 0 | 9 | 304:01:08 | 8 | 57:27:42 | 5.3x |
| 12 | 54:15:12 | 5.6x | |||
| 16 | 41:38:10 | 7.3x | |||
Conclusion
This article has presented a formal analysis of the Hybrid PQ TLS protocol with Maude-NPA and the parallel version of Maude-NPA. The most burdensome problem in the analysis is the big state space generated, which caused a long analysis time for our experiments. This problem, however, is not dedicated to Maude-NPA only, but rather the major drawback of other formal method tools based on exhaustive search. In fact, the running performance of Maude-NPA has significantly improved since several techniques have been proposed and implemented in the tool to reduce the size of the search space, such as generating formal grammars representing terms unreachable from initial states and using a super lazy intruder to delay the generation of substitution instances as much as possible (Escobar, Meadows & Meseguer, 2008). Moreover, using the parallel version of Maude-NPA allows us to obtain a better running performance than the original tool in this formal analysis case study.
To prepare for secure information communication once practical quantum computers become available, security analysis by formal methods is a useful approach to the verification and construction of secure post-quantum cryptosystems. Security verification by Maude-NPA on the one hand is fully automated, that is no manual effort is required once the formal specification and the attack pattern are provided. On the other hand, it may take a quite long time if the state space of the system under verification is huge (i.e., state explosion). One possible way to mitigate the analysis time is by introducing some never patterns serving as auxiliary lemmas to discard some useless reachability branches. This technique has been demonstrated through the case studies by González-Burgueño et al. (2014); González-Burgueño et al. (2015). The technique would be one piece of our future work to investigate on. Besides, we are also interested in formal verifications of post-quantum cryptographic protocols using some interactive approaches that require manual efforts from human users. The CafeOBJ/proof score approach (Ogata & Futatsugi, 2013; Ogata & Futatsugi, 2003) is such a promising method. We plan to integrate the two approaches to make the best use of the benefits obtained from them and mitigate their weak points.
Additional Information and Declarations
Competing Interests
The authors declare that there are no competing interests.
Author Contributions
Duong Dinh Tran conceived and designed the experiments, performed the experiments, analyzed the data, performed the computation work, prepared figures and/or tables, authored or reviewed drafts of the article, and approved the final draft.
Canh Minh Do conceived and designed the experiments, performed the experiments, analyzed the data, performed the computation work, prepared figures and/or tables, authored or reviewed drafts of the article, and approved the final draft.
Santiago Escobar conceived and designed the experiments, analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Kazuhiro Ogata conceived and designed the experiments, analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Data Deposition
The following information was supplied regarding data availability:
The complete protocol specification and the attack patterns are available at Zenodo:
duongtd23. (2023). Hybrid Post-Quantum TLS formal analysis in Maude-NPA (v1.1). Zenodo. https://doi.org/10.5281/zenodo.7919153.
Funding
This work was supported by the JST SICORP (No. JPMJSC20C2), the European Regional Development Fund, the Generalitat Valenciana, and the European Union NextGenerationEU. There was no additional external funding received for this study. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.