We have discussed AVL insertion in the previous post. In this post, we will follow a similar approach for deletion.
Steps to follow for deletion.
To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
- Left Rotation
- Right Rotation
T1, T2 and T3 are subtrees of the tree rooted with y (on left side)
or x (on right side)
y x
/ \ Right Rotation / \
x T3 – - – - – - – > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Let w be the node to be deleted
- Perform standard BST delete for w.
- Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the larger height child of z, and x be the larger height child of y. Note that the definitions of x and y are different from insertion here.
- Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
- y is left child of z and x is left child of y (Left Left Case)
- y is left child of z and x is right child of y (Left Right Case)
- y is right child of z and x is right child of y (Right Right Case)
- y is right child of z and x is left child of y (Right Left Case)
Like insertion, following are the operations to be performed in above mentioned 4 cases. Note that, unlike insertion, fixing the node z won’t fix the complete AVL tree. After fixing z, we may have to fix ancestors of z as well (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Unlike insertion, in deletion, after we perform a rotation at z, we may have to perform a rotation at ancestors of z. Thus, we must continue to trace the path until we reach the root.
Example:
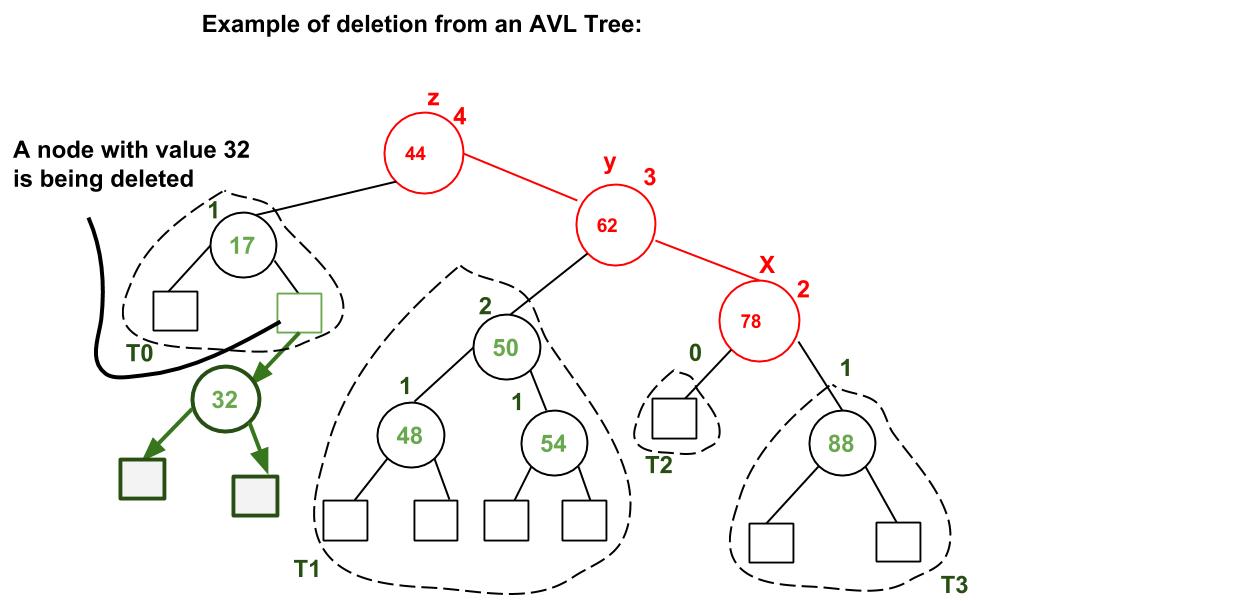
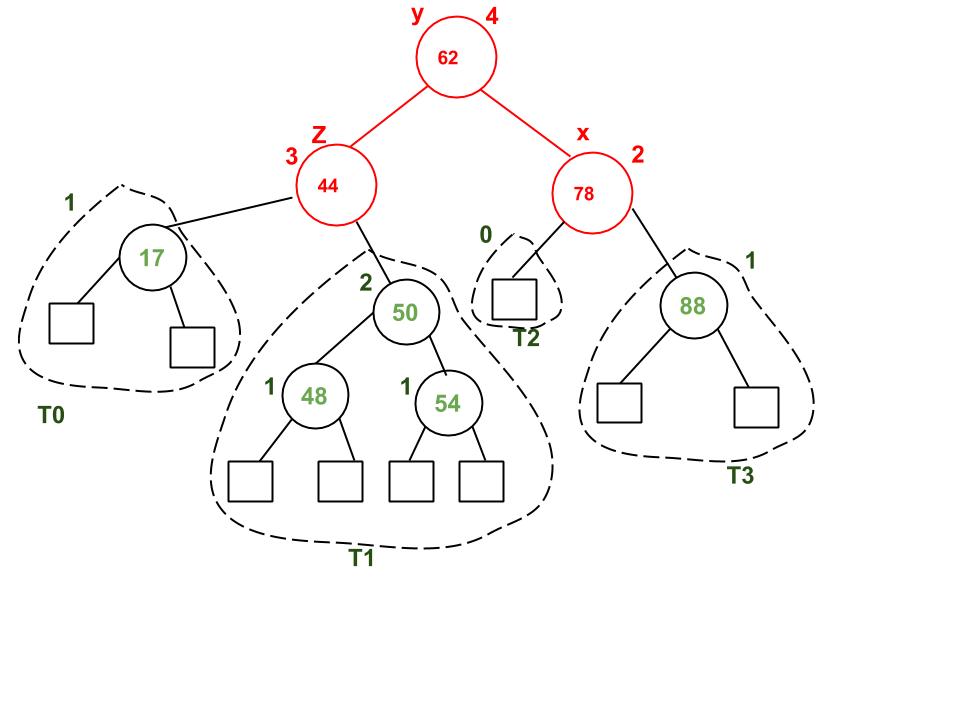
A node with value 32 is being deleted. After deleting 32, we travel up and find the first unbalanced node which is 44. We mark it as z, its higher height child as y which is 62, and y’s higher height child as x which could be either 78 or 50 as both are of same height. We have considered 78. Now the case is Right Right, so we perform left rotation.
Following is the implementation for AVL Tree Deletion. The following implementation uses the recursive BST delete as basis. In the recursive BST delete, after deletion, we get pointers to all ancestors one by one in bottom up manner. So we don’t need parent pointer (or reference) to travel up. The recursive code itself travels up and visits all the ancestors of the deleted node.
- Perform the normal BST deletion.
- The current node must be one of the ancestors of the deleted node. Update the height of the current node.
- Get the balance factor (left subtree height – right subtree height) of the current node.
- If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or Left Right case. To check whether it is Left Left case or Left Right case, get the balance factor of left subtree. If balance factor of the left subtree is greater than or equal to 0, then it is Left Left case, else Left Right case.
- If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right Left case. To check whether it is Right Right case or Right Left case, get the balance factor of right subtree. If the balance factor of the right subtree is smaller than or equal to 0, then it is Right Right case, else Right Left case.
C++
#include <bits/stdc++.h>
using namespace std;
// An AVL tree node
class Node {
public:
int key;
Node *left;
Node *right;
int height;
Node(int k) {
key = k;
left = nullptr;
right = nullptr;
height = 1;
}
};
// A utility function to get the height
// of the tree
int height(Node *N) {
if (N == nullptr)
return 0;
return N->height;
}
// A utility function to right rotate
// subtree rooted with y
Node *rightRotate(Node *y) {
Node *x = y->left;
Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = 1 + max(height(y->left),
height(y->right));
x->height = 1 + (height(x->left),
height(x->right));
// Return new root
return x;
}
// A utility function to left rotate
// subtree rooted with x
Node *leftRotate(Node *x) {
Node *y = x->right;
Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = 1 + max(height(x->left),
height(x->right));
y->height = 1 + max(height(y->left),
height(y->right));
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(Node *N) {
if (N == nullptr)
return 0;
return height(N->left) -
height(N->right);
}
Node* insert(Node* node, int key) {
// 1. Perform the normal BST rotation
if (node == nullptr)
return new Node(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys not allowed
return node;
// 2. Update height of this ancestor node
node->height = 1 + max(height(node->left),
height(node->right));
// 3. Get the balance factor of this
// ancestor node to check whether this
// node became unbalanced
int balance = getBalance(node);
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key) {
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key) {
node->right = rightRotate(node->right);
return leftRotate(node);
}
// return the (unchanged) node pointer
return node;
}
// Given a non-empty binary search tree,
// return the node with minimum key value
// found in that tree. Note that the entire
// tree does not need to be searched.
Node * minValueNode(Node* node) {
Node* current = node;
// loop down to find the leftmost leaf
while (current->left != nullptr)
current = current->left;
return current;
}
// Recursive function to delete a node with
// given key from subtree with given root.
// It returns root of the modified subtree.
Node* deleteNode(Node* root, int key) {
// STEP 1: PERFORM STANDARD BST DELETE
if (root == nullptr)
return root;
// If the key to be deleted is smaller
// than the root's key, then it lies in
// left subtree
if (key < root->key)
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater
// than the root's key, then it lies in
// right subtree
else if (key > root->key)
root->right = deleteNode(root->right, key);
// if key is same as root's key, then
// this is the node to be deleted
else {
// node with only one child or no child
if ((root->left == nullptr) ||
(root->right == nullptr)) {
Node *temp = root->left ?
root->left : root->right;
// No child case
if (temp == nullptr) {
temp = root;
root = nullptr;
} else // One child case
*root = *temp; // Copy the contents of
// the non-empty child
free(temp);
} else {
// node with two children: Get the
// inorder successor (smallest in
// the right subtree)
Node* temp = minValueNode(root->right);
// Copy the inorder successor's
// data to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
}
// If the tree had only one node then return
if (root == nullptr)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(height(root->left),
height(root->right));
// STEP 3: GET THE BALANCE FACTOR OF THIS
// NODE (to check whether this node
// became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if (balance > 1 &&
getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 &&
getBalance(root->left) < 0) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 &&
getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 &&
getBalance(root->right) > 0) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder
// traversal of the tree.
void preOrder(Node *root) {
if (root != nullptr) {
cout << root->key << " ";
preOrder(root->left);
preOrder(root->right);
}
}
// Driver Code
int main() {
Node *root = nullptr;
// Constructing tree given in the
// above figure
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
cout << "Preorder traversal of the "
"constructed AVL tree is \n";
preOrder(root);
root = deleteNode(root, 10);
cout << "\nPreorder traversal after"
" deletion of 10 \n";
preOrder(root);
return 0;
}
// C program to delete a node from AVL Tree
#include<stdio.h>
#include<stdlib.h>
// An AVL tree node
struct Node
{
int key;
struct Node *left;
struct Node *right;
int height;
};
// A utility function to get maximum of two integers
int max(int a, int b);
// A utility function to get height of the tree
int height(struct Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a new node with the given key and
NULL left and right pointers. */
struct Node* newNode(int key)
{
struct Node* node = (struct Node*)
malloc(sizeof(struct Node));
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially added at leaf
return(node);
}
// A utility function to right rotate subtree rooted with y
// See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
struct Node *x = y->left;
struct Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left), height(y->right))+1;
x->height = max(height(x->left), height(x->right))+1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x
// See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
struct Node *y = x->right;
struct Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left), height(x->right))+1;
y->height = max(height(y->left), height(y->right))+1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(struct Node *N)
{
if (N == NULL)
return 0;
return height(N->left) - height(N->right);
}
struct Node* insert(struct Node* node, int key)
{
/* 1. Perform the normal BST rotation */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys not allowed
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));
/* 3. Get the balance factor of this ancestor
node to check whether this node became
unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree, return the
node with minimum key value found in that tree.
Note that the entire tree does not need to be
searched. */
struct Node * minValueNode(struct Node* node)
{
struct Node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
current = current->left;
return current;
}
// Recursive function to delete a node with given key
// from subtree with given root. It returns root of
// the modified subtree.
struct Node* deleteNode(struct Node* root, int key)
{
// STEP 1: PERFORM STANDARD BST DELETE
if (root == NULL)
return root;
// If the key to be deleted is smaller than the
// root's key, then it lies in left subtree
if ( key < root->key )
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the
// root's key, then it lies in right subtree
else if( key > root->key )
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is
// the node to be deleted
else
{
// node with only one child or no child
if( (root->left == NULL) || (root->right == NULL) )
{
struct Node *temp = root->left ? root->left :
root->right;
// No child case
if (temp == NULL)
{
temp = root;
root = NULL;
}
else // One child case
*root = *temp; // Copy the contents of
// the non-empty child
free(temp);
}
else
{
// node with two children: Get the inorder
// successor (smallest in the right subtree)
struct Node* temp = minValueNode(root->right);
// Copy the inorder successor's data to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
}
// If the tree had only one node then return
if (root == NULL)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(height(root->left),
height(root->right));
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to
// check whether this node became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root->left) < 0)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder traversal of
// the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
if(root != NULL)
{
printf("%d ", root->key);
preOrder(root->left);
preOrder(root->right);
}
}
/* Driver program to test above function*/
int main()
{
struct Node *root = NULL;
/* Constructing tree given in the above figure */
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
/* The constructed AVL Tree would be
9
/ \
1 10
/ \ \
0 5 11
/ / \
-1 2 6
*/
printf("Preorder traversal of the constructed AVL "
"tree is \n");
preOrder(root);
root = deleteNode(root, 10);
/* The AVL Tree after deletion of 10
1
/ \
0 9
/ / \
-1 5 11
/ \
2 6
*/
printf("\nPreorder traversal after deletion of 10 \n");
preOrder(root);
return 0;
}
class Node {
int key;
Node left, right;
int height;
Node(int k) {
key = k;
left = right = null;
height = 1;
}
}
public class Main {
// A utility function to get the height
// of the tree
static int height(Node N) {
if (N == null)
return 0;
return N.height;
}
// A utility function to right rotate
// subtree rooted with y
static Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
// Perform rotation
x.right = y;
y.left = T2;
// Update heights
y.height = Math.max(height(y.left),
height(y.right)) + 1;
x.height = Math.max(height(x.left),
height(x.right)) + 1;
// Return new root
return x;
}
// A utility function to left rotate
// subtree rooted with x
static Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
// Perform rotation
y.left = x;
x.right = T2;
// Update heights
x.height = Math.max(height(x.left),
height(x.right)) + 1;
y.height = Math.max(height(y.left),
height(y.right)) + 1;
// Return new root
return y;
}
// Get Balance factor of node N
static int getBalance(Node N) {
if (N == null)
return 0;
return height(N.left) - height(N.right);
}
static Node insert(Node node, int key) {
// 1. Perform the normal BST insertion
if (node == null)
return new Node(key);
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
else // Duplicate keys not allowed
return node;
// 2. Update height of this ancestor node
node.height = Math.max(height(node.left),
height(node.right)) + 1;
// 3. Get the balance factor of this node
// to check whether this node became
// unbalanced
int balance = getBalance(node);
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if (balance > 1 && key < node.left.key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node.right.key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// Given a non-empty binary search tree,
// return the node with minimum key value
// found in that tree.
static Node minValueNode(Node node) {
Node current = node;
// loop down to find the leftmost leaf
while (current.left != null)
current = current.left;
return current;
}
// Recursive function to delete a node with
// given key from subtree with given root.
// It returns root of the modified subtree.
static Node deleteNode(Node root, int key) {
// STEP 1: PERFORM STANDARD BST DELETE
if (root == null)
return root;
// If the key to be deleted is smaller
// than the root's key, then it lies in
// left subtree
if (key < root.key)
root.left = deleteNode(root.left, key);
// If the key to be deleted is greater
// than the root's key, then it lies in
// right subtree
else if (key > root.key)
root.right = deleteNode(root.right, key);
// if key is same as root's key, then
// this is the node to be deleted
else {
// node with only one child or no child
if ((root.left == null) ||
(root.right == null)) {
Node temp = root.left != null ?
root.left : root.right;
// No child case
if (temp == null) {
temp = root;
root = null;
} else // One child case
root = temp; // Copy the contents of
// the non-empty child
} else {
// node with two children: Get the
// inorder successor (smallest in
// the right subtree)
Node temp = minValueNode(root.right);
// Copy the inorder successor's
// data to this node
root.key = temp.key;
// Delete the inorder successor
root.right = deleteNode(root.right, temp.key);
}
}
// If the tree had only one node then return
if (root == null)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.height = Math.max(height(root.left),
height(root.right)) + 1;
// STEP 3: GET THE BALANCE FACTOR OF THIS
// NODE (to check whether this node
// became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then
// there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root.left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root.right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder
// traversal of the tree.
static void preOrder(Node root) {
if (root != null) {
System.out.print(root.key + " ");
preOrder(root.left);
preOrder(root.right);
}
}
// Driver Code
public static void main(String[] args) {
Node root = null;
// Constructing tree given in the
// above figure
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
System.out.println("Preorder traversal of the "
+ "constructed AVL tree is:");
preOrder(root);
root = deleteNode(root, 10);
System.out.println("\nPreorder traversal after"
+ " deletion of 10:");
preOrder(root);
}
}
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
def height(N):
if N is None:
return 0
return N.height
def right_rotate(y):
x = y.left
T2 = x.right
# Perform rotation
x.right = y
y.left = T2
# Update heights
y.height = max(height(y.left),
height(y.right)) + 1
x.height = max(height(x.left),
height(x.right)) + 1
# Return new root
return x
def left_rotate(x):
y = x.right
T2 = y.left
# Perform rotation
y.left = x
x.right = T2
# Update heights
x.height = max(height(x.left),
height(x.right)) + 1
y.height = max(height(y.left),
height(y.right)) + 1
# Return new root
return y
def get_balance(N):
if N is None:
return 0
return height(N.left) - height(N.right)
def insert(node, key):
# 1. Perform the normal BST insertion
if node is None:
return Node(key)
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
else: # Duplicate keys not allowed
return node
# 2. Update height of this ancestor node
node.height = max(height(node.left),
height(node.right)) + 1
# 3. Get the balance factor of this node
# to check whether this node became
# unbalanced
balance = get_balance(node)
# If this node becomes unbalanced, then
# there are 4 cases
# Left Left Case
if balance > 1 and key < node.left.key:
return right_rotate(node)
# Right Right Case
if balance < -1 and key > node.right.key:
return left_rotate(node)
# Left Right Case
if balance > 1 and key > node.left.key:
node.left = left_rotate(node.left)
return right_rotate(node)
# Right Left Case
if balance < -1 and key < node.right.key:
node.right = right_rotate(node.right)
return left_rotate(node)
return node
def min_value_node(node):
current = node
# loop down to find the leftmost leaf
while current.left is not None:
current = current.left
return current
def delete_node(root, key):
# STEP 1: PERFORM STANDARD BST DELETE
if root is None:
return root
# If the key to be deleted is smaller
# than the root's key, then it lies in
# left subtree
if key < root.key:
root.left = delete_node(root.left, key)
# If the key to be deleted is greater
# than the root's key, then it lies in
# right subtree
elif key > root.key:
root.right = delete_node(root.right, key)
# if key is same as root's key, then
# this is the node to be deleted
else:
# node with only one child or no child
if root.left is None or root.right is None:
temp = root.left if root.left else root.right
# No child case
if temp is None:
root = None
else: # One child case
root = temp
else:
# node with two children: Get the
# inorder successor (smallest in
# the right subtree)
temp = min_value_node(root.right)
# Copy the inorder successor's
# data to this node
root.key = temp.key
# Delete the inorder successor
root.right = delete_node(root.right, temp.key)
# If the tree had only one node then return
if root is None:
return root
# STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.height = max(height(root.left),
height(root.right)) + 1
# STEP 3: GET THE BALANCE FACTOR OF THIS
# NODE (to check whether this node
# became unbalanced)
balance = get_balance(root)
# If this node becomes unbalanced, then
# there are 4 cases
# Left Left Case
if balance > 1 and get_balance(root.left) >= 0:
return right_rotate(root)
# Left Right Case
if balance > 1 and get_balance(root.left) < 0:
root.left = left_rotate(root.left)
return right_rotate(root)
# Right Right Case
if balance < -1 and get_balance(root.right) <= 0:
return left_rotate(root)
# Right Left Case
if balance < -1 and get_balance(root.right) > 0:
root.right = right_rotate(root.right)
return left_rotate(root)
return root
def pre_order(root):
if root is not None:
print("{0} ".format(root.key), end="")
pre_order(root.left)
pre_order(root.right)
# Driver Code
if __name__ == "__main__":
root = None
# Constructing tree given in the
# above figure
root = insert(root, 9)
root = insert(root, 5)
root = insert(root, 10)
root = insert(root, 0)
root = insert(root, 6)
root = insert(root, 11)
root = insert(root, -1)
root = insert(root, 1)
root = insert(root, 2)
print("Preorder traversal of the "
"constructed AVL tree is")
pre_order(root)
root = delete_node(root, 10)
print("\nPreorder traversal after"
" deletion of 10")
pre_order(root)
using System;
class Node {
public int key;
public Node left;
public Node right;
public int height;
public Node(int k) {
key = k;
left = null;
right = null;
height = 1;
}
}
class Program {
static int height(Node N) {
if (N == null) return 0;
return N.height;
}
static Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
// Perform rotation
x.right = y;
y.left = T2;
// Update heights
y.height = Math.Max(height(y.left), height(y.right)) + 1;
x.height = Math.Max(height(x.left), height(x.right)) + 1;
// Return new root
return x;
}
static Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
// Perform rotation
y.left = x;
x.right = T2;
// Update heights
x.height = Math.Max(height(x.left), height(x.right)) + 1;
y.height = Math.Max(height(y.left), height(y.right)) + 1;
// Return new root
return y;
}
static int getBalance(Node N) {
if (N == null) return 0;
return height(N.left) - height(N.right);
}
static Node Insert(Node node, int key) {
// 1. Perform the normal BST insertion
if (node == null) return new Node(key);
if (key < node.key) {
node.left = Insert(node.left, key);
} else if (key > node.key) {
node.right = Insert(node.right, key);
} else { // Duplicate keys not allowed
return node;
}
// 2. Update height of this ancestor node
node.height = Math.Max(height(node.left), height(node.right)) + 1;
// 3. Get the balance factor of this node
// to check whether this node became unbalanced
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node.left.key) {
return rightRotate(node);
}
// Right Right Case
if (balance < -1 && key > node.right.key) {
return leftRotate(node);
}
// Left Right Case
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
static Node minValueNode(Node node) {
Node current = node;
// loop down to find the leftmost leaf
while (current.left != null) {
current = current.left;
}
return current;
}
static Node DeleteNode(Node root, int key) {
// STEP 1: PERFORM STANDARD BST DELETE
if (root == null) return root;
// If the key to be deleted is smaller
// than the root's key, then it lies in
// left subtree
if (key < root.key) {
root.left = DeleteNode(root.left, key);
} else if (key > root.key) {
root.right = DeleteNode(root.right, key);
} else { // if key is same as root's key
// node with only one child or no child
if (root.left == null || root.right == null) {
Node temp = root.left != null ? root.left : root.right;
// No child case
if (temp == null) {
root = null;
} else { // One child case
root = temp; // Copy the non-empty child
}
} else {
// node with two children: Get the inorder successor
Node temp = minValueNode(root.right);
// Copy the inorder successor's data to this node
root.key = temp.key;
// Delete the inorder successor
root.right = DeleteNode(root.right, temp.key);
}
}
// If the tree had only one node then return
if (root == null) return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.height = Math.Max(height(root.left), height(root.right)) + 1;
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE
int balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root.left) >= 0) {
return rightRotate(root);
}
// Left Right Case
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root.right) <= 0) {
return leftRotate(root);
}
// Right Left Case
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
static void PreOrder(Node root) {
if (root != null) {
Console.Write(root.key + " ");
PreOrder(root.left);
PreOrder(root.right);
}
}
// Driver Code
public static void Main(string[] args) {
Node root = null;
// Constructing tree given in the above figure
root = Insert(root, 9);
root = Insert(root, 5);
root = Insert(root, 10);
root = Insert(root, 0);
root = Insert(root, 6);
root = Insert(root, 11);
root = Insert(root, -1);
root = Insert(root, 1);
root = Insert(root, 2);
Console.WriteLine("Preorder traversal of the constructed AVL tree is:");
PreOrder(root);
root = DeleteNode(root, 10);
Console.WriteLine("\nPreorder traversal after deletion of 10:");
PreOrder(root);
}
}
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
this.height = 1;
}
}
function height(N) {
if (N === null) return 0;
return N.height;
}
function rightRotate(y) {
const x = y.left;
const T2 = x.right;
// Perform rotation
x.right = y;
y.left = T2;
// Update heights
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
// Return new root
return x;
}
function leftRotate(x) {
const y = x.right;
const T2 = y.left;
// Perform rotation
y.left = x;
x.right = T2;
// Update heights
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
// Return new root
return y;
}
function getBalance(N) {
if (N === null) return 0;
return height(N.left) - height(N.right);
}
function insert(node, key) {
// 1. Perform the normal BST insertion
if (node === null) return new Node(key);
if (key < node.key) {
node.left = insert(node.left, key);
} else if (key > node.key) {
node.right = insert(node.right, key);
} else { // Duplicate keys not allowed
return node;
}
// 2. Update height of this ancestor node
node.height = Math.max(height(node.left), height(node.right)) + 1;
// 3. Get the balance factor of this node
// to check whether this node became unbalanced
const balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node.left.key) {
return rightRotate(node);
}
// Right Right Case
if (balance < -1 && key > node.right.key) {
return leftRotate(node);
}
// Left Right Case
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
function minValueNode(node) {
let current = node;
// loop down to find the leftmost leaf
while (current.left !== null) {
current = current.left;
}
return current;
}
function deleteNode(root, key) {
// STEP 1: PERFORM STANDARD BST DELETE
if (root === null) return root;
// If the key to be deleted is smaller
// than the root's key, then it lies in
// left subtree
if (key < root.key) {
root.left = deleteNode(root.left, key);
} else if (key > root.key) {
root.right = deleteNode(root.right, key);
} else { // if key is same as root's key
// node with only one child or no child
if (root.left === null || root.right === null) {
const temp = root.left ? root.left : root.right;
// No child case
if (temp === null) {
root = null;
} else { // One child case
root = temp; // Copy the contents of the non-empty child
}
} else {
// node with two children: Get the inorder successor
const temp = minValueNode(root.right);
// Copy the inorder successor's data to this node
root.key = temp.key;
// Delete the inorder successor
root.right = deleteNode(root.right, temp.key);
}
}
// If the tree had only one node then return
if (root === null) return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root.height = Math.max(height(root.left), height(root.right)) + 1;
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE
const balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root.left) >= 0) {
return rightRotate(root);
}
// Left Right Case
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root.right) <= 0) {
return leftRotate(root);
}
// Right Left Case
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
function preOrder(root) {
if (root !== null) {
console.log(root.key + " ");
preOrder(root.left);
preOrder(root.right);
}
}
// Driver Code
let root = null;
// Constructing tree given in the above figure
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
console.log("Preorder traversal of the constructed AVL tree is:");
preOrder(root);
root = deleteNode(root, 10);
console.log("\nPreorder traversal after deletion of 10:");
preOrder(root);
OutputPreorder traversal of the constructed AVL tree is
5 1 0 -1 2 9 6 10 11
Preorder traversal after deletion of 10
5 1 0 -1 2 9 6 11
Output:
Preorder traversal of the constructed AVL tree is
9 1 0 -1 5 2 6 10 11
Preorder traversal after deletion of 10
1 0 -1 9 5 2 6 11
Time Complexity: The rotation operations (left and right rotate) take constant time as only few pointers are being changed there. Updating the height and getting the balance factor also take constant time. So the time complexity of AVL delete remains same as BST delete which is O(h) where h is height of the tree. Since AVL tree is balanced, the height is O(log n). So time complexity of AVL delete is O(log n).
Auxiliary Space: O(log n) for recursion call stack as we have written a recursive method to delete
Summary of AVL Trees
- These are self-balancing binary search trees.
- Balancing Factor ranges -1, 0, and +1.
- When balancing factor goes beyond the range require rotations to be performed
- Insert, delete, and search time is O(log N).
- AVL tree are mostly used where search is more frequent compared to insert and delete operation.