Open In App

Mensuration in Maths | Formulas for 2D and 3D Shapes, Examples

Last Updated : 31 Jul, 2024
Summarize
Comments
Improve
Suggest changes
Like Article
Like
Save
Share
Report
News Follow

Mensuration is a branch of mathematics concerned with the calculation of geometric figures and their parameters such as weight, volume, form, surface area, lateral surface area, and so on.

Let’s learn about all the mensuration formulas in maths.

Mensuration Meaning

Mensuration is the branch of mathematics that deals with the measurement of various geometric figures and shapes. This includes calculating areas, volumes, and perimeters of two-dimensional shapes like squares, rectangles, circles, and triangles, as well as three-dimensional figures like cubes, cylinders, spheres, and cones.

These shapes can exist in 2 ways:

  • Two-Dimensional Shapes – circle, triangle, square, etc.
  • Three-Dimensional Shapes – cube, cuboid, cone, etc.

Difference Between 2D and 3D Shapes

2-Dimensional vs 3-Dimensional Shapes
2D Shape 3D Shape
Any shape is 2D if it is bound by three or more straight lines in a plane. A shape is a three-dimensional shape if there are several surfaces or planes around it.
There is no height or depth in these shapes. In contrast to 2D forms, these are sometimes known as solid shapes and have height or depth.
These shapes just have length and width as their dimensions. Since they have depth (or height), breadth, and length, they are referred to as three-dimensional objects.
We can calculate their perimeter and area. Their volume, curved surface area, lateral surface area, or total surface area can all be calculated.

Mensuration Terminologies

Here is the list of terms you will come across in mensuration class. We have provided the term, it’s abbreviation, unit and definition for easy understanding.

Terms Abbreviation Unit Definition
Area A m2 or cm2 The surface that the closed form covers is known as the area.
Perimeter P cm or m A perimeter is the length of the continuous line that encircles the specified figure.
Volume V cm3 or m3 A 3D shape’s space is referred to as its volume.
Curved Surface Area CSA m2 or cm2 The overall area is known as a Curved surface area if there is a curved surface. Example: Sphere
Lateral Surface area LSA m2 or cm2 The term “Lateral Surface area” refers to the combined area of all lateral surfaces that encircle the provided figure.
Total Surface Area TSA m2 or cm2 The total surface area is the total of all the curved and lateral surface areas.
Square Unit – m2 or cm2 A square unit is the area that a square of side one unit covers.
Cube Unit – m3 or cm3 The space taken up by a cube with a single side.

Mensuration Formula For 2D Shapes

The following table provides a list of all mensuration formulas for 2D shapes:

Shape Area (Square units) Perimeter (units) Figure
Square a2 4a
Square Formula

Square dimensions
Rectangle l × b 2 (l + b)
Rectangle Formula

rectangle dimensions
Circle πr2 2 π r
Circle Formula

circle with radius
Scalene Triangle √[s(s−a)(s−b)(s−c)],
Where, s = (a+b+c)/2		 a+b+c
Scalene Triangle Formula

Scalene triangle dimensions
Isosceles Triangle ½ × b × h 2a + b
Isosceles Triangle

isosceles triangle dimensions
Equilateral Triangle (√3/4) × a2 3a
Equilateral Triangle

Equilateral triangle dimensions
Right Angle Triangle ½ × b × h
b + hypotenuse + h
Right Angled Triangle

Right Angle Triangle dimensions
Rhombus ½ × d1 × d2 4 × side Rhombus Formula
Parallelograms b × h 2(l+b)
Parallelogram Formula

Parallelogram dimensions
Trapezium ½ h(a+c) a+b+c+d
Trapezium Formula

Trapezium dimensions

Learn More:

Mensuration Formula for 3D Shapes

The following table provides a list of all mensuration formulas for 3D shapes:

Shape Volume (Cubic units) Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) Total Surface Area (TSA) (Square units) Figure
Cube a3 LSA = 4 a2 6 a2
Cube

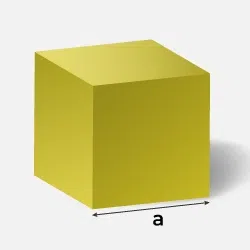cube dimensions
Cuboids l × b × h LSA = 2h(l + b) 2 (lb +bh +hl)
Cuboid

cuboid dimensions
Sphere (4/3) π r3 4 π r2 4 π r2
Sphere

sphere dimensions
Hemisphere (⅔) π r3 2 π r2 3 π r2
Hemisphere

hemisphere dimensions
Cylinder π r 2 h 2π r h 2πrh + 2πr2
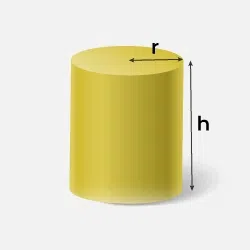Cylinder

cylinder dimensions
Cone (⅓) π r2 h π r l πr (r + l) Cone

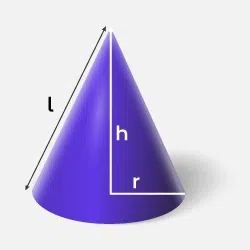Learn More :

Solved Problems on Mensuration

Let’s solve some example problems on mensuration.

Problem 1: Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.

Solution:

Radius of the cone, r = 1.5 cm

Height of the cone, h = 5 cm

∴ Volume of the cone, V = 13πr2h=13×227×(1.5)2×5= 11.79 cm3

Thus, the volume of the cone is 11.79 cm3. 

Problem 2: The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.

Solution:

The dimensions of the cuboid are 44 cm, 21 cm and 12 cm.

Let the radius of the cone be r cm.

Height of the cone, h = 24 cm

It is given that cuboid is melted to form a cone.

∴ Volume of metal in cone = Volume of metal in cuboid

⇒(1/3)πr2h=44×21×12             

 (Volume of cuboid=Length×Breadth×Height)

⇒(1/3)×(22/7)×r2×24=44×21×12

⇒r= √(44×21×12×21) / (22×24)

=21 cm

Thus, the radius of the base of cone is 21 cm.
 

Problem 3: The radii of two circular ends of frustum shape bucket are 14 cm and 7 cm. The height of the bucket is 30 cm. How many liters of water can it hold? (1 litre = 1000 cm3).

Solution:

Radius of one circular end, r1 = 14 cm

Radius of other circular end, r2 = 7 cm

Height of the bucket, h = 30 cm

∴ Volume of water in the bucket = Volume of frustum of cone
=(1/3)Ï€h(r12+r1r2+r22)

=13×22/7×30×(142+14×7+72)

=13×22/7×30×343=10780 cm3

=107801000=10.780 L

Thus, the bucket can hold 10.780 litres of water.

FAQs On Mensuration

What is Mensuration?

Mensuration deals with the calculation of geometric figures and their parameters such as weight, volume, form, surface area, lateral surface area, and so on.

What are 2D and 3D Shapes?

Any shape is considered to be 2D if it is bound by three or more straight lines in a plane whereas a shape is a three-dimensional shape if there are several surfaces or planes around it.

What is Area of Cylinder Formula?

Lateral or Curved Surface area of a cylinder = 2Ï€ r h

Total Surface Area of a cylinder = 2Ï€rh + 2Ï€r2

What is TSA (Total Surface Area) of Sphere Formula?

Area of Sphere is given by the following formula :

A= 4 π r2

What is Volume of Cone Formula?

Volume of Cone is given by the following formula :

V= (⅓) π r2 h

What is Area of Triangle Formula?

Area of Triangle is given by the following formula :

A= 1/2 ×b ×h

What is Area of Circle Formula?

Area of Circle is given by the following formula :

A= π r2

What is Volume of Cylinder Formula?

Volume of Cylinder is given by the following formula :

V= π r 2 h



https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
News
Improve
Next Article
Geometric Shapes in Maths

Similar Reads

Sphere: Definition, Formulas, Examples, Shapes, Properties
Sphere is a three-dimensional object that is perfectly round and symmetrical in shape. It is a set of points in 3-D space that are all equidistant from a fixed point(center). The distance from the center to any point on the surface of the sphere is the same, and this distance is called the radius. A sphere is defined in 3 axis whereas a sphere is d
10 min read
Mensuration Formulas
Mensuration is the branch of geometry that deals with the measurement of area, length, or volume in 2D and 3D shapes. The 2D and 3D shapes are often called geometric shapes. In this article, we have curated all the mensuration formulas for various 2-D and 3-D shapes in detail. Mensuration DefinitionMensuration is measuring various parameters of 2-D
12 min read
Perimeter Formulas for Geometric Shapes
Perimeter Formulas are the mathematical Formulas used to calculate the total boundary length of any geometrical shape. In mathematics or in daily lives geometry and geometrical shapes always play an essential role. Starting from a simple tray to a big building, we are always surrounded by geometry in different shapes and sizes. The shape and surfac
7 min read
Volume Formulas for 3D Shapes
In this article, we will learn how to calculate volume for different 3-D shapes and their Volume formulas examples in detail. Table of Content What is Volume?Volume of CubeVolume of CuboidVolume of ConeVolume of CylinderVolume of SphereVolume of HemisphereVolume of Prism Volume of PyramidExamples on Volume FormulaPractice Questions on Volume Formul
8 min read
Mensuration - Volume of Cube, Cuboid, and Cylinder | Class 8 Maths
Mensuration is the branch of mathematics which deals with the study of different geometrical shapes, their areas, and volume. It uses geometric calculations and algebraic equations to compute the measurement of various aspects of objects like Surface Area, Volume, etc.  Volume is the measurement of the amount of space inside a 3D object that can be
4 min read
Volume and Capacity - Mensuration | Class 8 Maths
Mensuration is the branch of mathematics that talks about the length, volume, and area of different geometrical objects. The shape may be in 2-D or 3-D. We find the volume of 3-D objects and the area of 2-D objects. Table of Content What is Volume?What is Capacity?Mensuration of Some Enclosed FiguresCubeCuboidCylinder ConeFormulas for Common Geomet
9 min read
Trigonometry Formulas - List of All Trigonometric Identities and Formulas
Trigonometry formulas are equations that relate the sides and angles of triangles. They are essential for solving a wide range of problems in mathematics, physics, engineering and other fields. Here are some of the most common types of trigonometry formulas: Basic definitions: These formulas define the trigonometric ratios (sine, cosine, tangent, e
10 min read
Trapezium in Maths | Formulas, Properties & Examples
Trapezium in Maths: A Trapezium is a polygon with four sides, i.e. it is a quadrilateral. Trapezium originated from the Greek word "trapeze" which means table. It is a complex quadrilateral. A trapezium is a special quadrilateral with only one pair of parallel sides. A trapezium is a two-dimensional shape that appears as a table. A trapezium has fo
12 min read
Mapping Space Around Us - Visualizing Solid Shapes | Class 8 Maths
In Geometry, 3D shapes are known as three-dimensional shapes or solids, or solid shapes. 3D shapes or solid shapes have three different measures such as length, width, and height as its dimensions. A polygon is a 2D shape with straight sides. A regular shape has all sides the same length and all interior angles the same size. An irregular shape has
7 min read
Geometric Shapes in Maths
Geometric Shapes: Geometric shapes are the figures used in mathematics to represent the forms of real-world things. Shapes are the forms of things in geometry that have boundaries, angles, and surfaces. There are two types of geometric figures: 2D Shapes(Two-dimensional)3D Shapes(Three-dimensional)Shapes are also divided into two types based on the
5 min read
Area Formulas in Maths
Area Formulas for various objects are the formulas that are used to find the area of various object. Area formulas are essential for calculating the area of various geometric figures and are widely used in mathematics, engineering, architecture, and many other fields. Area formulas of various geometric shapes are dependent on various parameters, su
10 min read
Area and Perimeter of Shapes | Formula and Examples
Area and Perimeter are the two fundamental properties related to 2-dimensional shapes. Defining the size of the shape and the length of its boundary. By learning about the areas of 2D shapes, we can easily determine the surface areas of 3D bodies and the perimeter helps us to calculate the length of the boundary of any 2D closed shape. In this arti
11 min read
Special Series in Maths - Sequences and Series | Class 11 Maths
Special Series: A series can be defined as the sum of all the numbers of the given sequence. The sequences are finite as well as infinite. In the same way, the series can also be finite or infinite. For example, consider a sequence as 1, 3, 5, 7, … Then the series of these terms will be 1 + 3 + 5 + 7 + ….. The series special in some way or the othe
10 min read
Difference Between Maths and Vedic Maths
Mathematics has been a fundamental part of human knowledge for centuries, evolving through various cultures and eras. In the modern world, we primarily rely on what is known as Modern Mathematics—a structured and systematic approach to solving mathematical problems using algebra, geometry, calculus, and more. However, another fascinating system, Ve
6 min read
Polyhedron | Meaning, Shapes, Formula, and Examples
A polyhedron is a three-dimensional shape with flat polygonal faces, straight edges, and sharp vertices. Examples include cubes, prisms, and pyramids. However, shapes such as cones and spheres do not qualify as polyhedrons because they lack polygonal faces. It can have any polygon such as a triangle, pentagon, hexagon, etc. as faces as well and it
9 min read
Class 8 RD Sharma Solutions - Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube) - Exercise 21.1 | Set 1
Question 1: Find the volume of cuboid whose: i) length = 12 cm, breadth = 8 cm and height = 6 cm ii) length = 1.2 m, breadth = 30 cm and height = 15 cm iii) length = 1.5 dm, breadth = 2.5 dm and height = 8 cm Solution: i) The details given about cuboid are - Length of cuboid = 12 cm Breadth of cuboid = 8 cm Height of cuboid = 6 cm Volume of cuboid
8 min read
Class 8 RD Sharma Solutions - Chapter 21 Mensuration II (Volume and Surface Areas of a Cuboid and a Cube) - Exercise 21.1 | Set 2
Chapter 21 Mensuration II (Volume and Surface Areas of a Cuboid and a Cube) - Exercise 21.1 | Set 1Question 12: A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it beads of volume 1.5 cm3 each are to be made. Find the number of beads that can be made from the block. Solution: The details given about cuboidal block of s
7 min read
Class 8 RD Sharma Solutions - Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube) - Exercise- 21.2 | Set 2
Question 11. How many bricks each of size 25 cm x 10 cm x 8 cm will be required to build a wall 5 m long, 3 m high, and 16 cm thick assuming that the volume of sand and cement used in the construction is negligible? Solution: Given, length of brick = 25 cm The breadth of brick = 10 cm The height of brick = 8 cm So, the volume of 1 brick = l × b × h
7 min read
Class 8 RD Sharma - Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube) - Exercise 21.3 | Set 1
Question 1. Find the surface area of a cuboid whose (i) length = 10 cm, breadth = 12 cm, height = 14 cm(ii) length = 6 dm, breadth = 8 dm, height = 10 dm(iii) length = 2 m, breadth = 4 m, height = 5 m(iv) length = 3.2 m, breadth = 30 dm, height = 250 cm. Solution : i) length = 10 cm, breadth = 12 cm, height = 14 cm Given, the Length of cuboid = 10
8 min read
Class 8 RD Sharma - Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube) - Exercise 21.3 | Set 2
Question 10. A classroom is 11 m long, 8 m wide, and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows, etc.)? Solution: Given, the Length of classroom = 11 m The Breadth of classroom = 8 m The Height of the classroom = 5 m Area of floor = length × breadth = 11 × 8 = 88 m2 And, the Area of four walls (inc
7 min read
Class 8 RD Sharma Solutions- Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube)- Exercise 21.4 | Set 2
Question 11. A field is 150m long and 100m wide. A plot (outside the field) 50m long and 30m wide is dug to a depth of 8m and the earth taken out from the plot is spread evenly in the field. By how much is the level of field raised? Solution: Given, the length of field = 150 m The width of the field = 100 m So, the area of field = Length × breadth
8 min read
Class 8 RD Sharma Solutions- Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube)- Exercise 21.2 | Set 1
Question 1. Find the volume in cubic meters (cu.m) of each of the cuboids whose dimensions are :(i) length = 12 m, breadth = 10 m, height = 4.5 m(ii) length = 4 m, breadth = 2.5 m, height = 50 cm(iii) length = 10 m, breadth = 25 dm, height = 25 cmSolution: i) length = 12 m, breadth = 10 m, height = 4.5 m Since, Length (l) = 12 m Breadth (b) = 10 m
6 min read
Class 8 RD Sharma Solutions - Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube)- Exercise 21.4 | Set 1
This article provides step-by-step solutions to all the questions in the Exercise 21.4 | Set 1 of Class 8 RD Sharma Book of Chapter 21 Mensuration II (Volumes and Surface Areas of a Cuboid and a Cube). This exercise deals with the volumes and surface areas of cuboids and cubes, which are fundamental concepts in geometry and have practical applicati
8 min read
Class 8 RD Sharma Solutions- Chapter 22 Mensuration III (Surface Area And Volume Of Right Circular Cylinder) - Exercise 22.2 | Set 1
Question 1. Find the volume of a cylinder whose (i) r = 3.5 cm, h = 40 cm (ii) r = 2.8 m, h = 15 m Solution: (i) Given that, r = 3.5 cm, h = 40 cm As we know that Volume of a cylinder = πr2h = 22/7 × 3.5 × 3.5 × 40 = 1540 cm3 (ii) Given that, r = 2.8 m, h =15 m As we know that Volume of a cylinder = πr2h = 22/7 × 2.8 × 2.8 × 15 = 369.6 m3 Question
11 min read
Class 8 RD Sharma Solutions- Chapter 22 Mensuration III (Surface Area And Volume Of Right Circular Cylinder) - Exercise 22.2 | Set 2
Chapter 22 Mensuration III (Surface Area And Volume Of Right Circular Cylinder) - Exercise 22.2 | Set 1Question 21. A well is dug 20 m deep and it has a diameter of 7 m. The earth which is so dug out is spread out on a rectangular plot 22 m long and 14 m broad. What is the height of the platform so formed? Solution: Given that, Depth of well = 20m
15+ min read
Class 8 RD Sharma Solutions - Chapter 22 Mensuration III (Surface Area And Volume Of Right Circular Cylinder) - Exercise 22.1 | Set 1
Chapter 22 of RD Sharma's Class 8 Mathematics textbook, titled "Mensuration III," focuses on the surface area and volume of right circular cylinders. Exercise 22.1 | Set 1 specifically deals with calculating the curved surface area, total surface area, and volume of cylinders. This exercise introduces students to the fundamental formulas and concep
8 min read
Class 8 RD Sharma Solutions - Chapter 22 Mensuration III (Surface Area And Volume Of Right Circular Cylinder) - Exercise 22.1 | Set 2
Chapter 22 of RD Sharma's Class 8 Mathematics textbook delves into the fascinating world of mensuration, specifically focusing on the surface area and volume of right circular cylinders. This chapter builds upon students' previous knowledge of geometry and introduces them to more complex three-dimensional shapes. The chapter covers various aspects
9 min read
Derivatives | First and Second Order Derivatives, Formulas and Examples
Derivatives: In mathematics, a Derivative represents the rate at which a function changes as its input changes. It measures how a function's output value moves as its input value nudges a little bit. This concept is a fundamental piece of calculus. It is used extensively across science, engineering, economics, and more to analyze changes. Table of
15+ min read
Important Mensuration Questions
Mensuration means measuring shapes like squares, circles, and triangles. In this article, we'll help you understand Mensuration questions and provide simple answers. Whether you're a student getting ready for tests or just want to get better at math, you'll find easy explanations and step-by-step solutions. In this article, we'll cover important to
8 min read
NCERT Solutions Class 8 – Chapter 9 Mensuration – Exercise 9.1
Question 1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and the perpendicular distance between them is 0.8 m.Solution:  One parallel side of the trapezium (a) = 1 m And second side (b) = 1.2 m and height (h) = 0.8 m Area of top surface of the table = (½) × (a + b)h = (½) × (1 + 1.2)0
7 min read
Article Tags :
three90RightbarBannerImg
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox