Geometry

Geometry is the branch of mathematics that deals with the shapes, angles, dimensions, and sizes of various things that we see in everyday life. Geometry is derived from Ancient Greek words – ‘Geo’ which means ‘Earth’ and ‘metron’ which means ‘measurement’.

In this article, you will learn everything related to Geometry, including, different types of geometry, examples, and its applications in real life, etc.

What is Geometry in Maths?

Geometry is a branch of mathematics that studies the properties, measurement, and relationships of points, lines, angles, surfaces, and solids.

Geometry is the study of different varieties of shapes, figures, and sizes. It gives us knowledge about distances, angles, patterns, areas, and volumes of shapes. It is mainly divided into plane and solid geometry. In plane geometry, 2d shapes such as triangles, squares, rectangles, and circles are studied. Whereas, in solid geometry, 3d shapes such as cubes, cuboids, cones, etc. are studied. The basic geometry is based on points, lines, and planes explained in coordinate geometry. 

Its principles depend on points, lines, angles, and planes. All the geometrical shapes are based on these geometrical concepts.

Branches of Geometry

The geometry can be divided into different parts:

• Algebraic Geometry
• Discrete Geometry
• Differential Geometry
• Euclidean Geometry
• Non-Euclidean Geometry (Elliptical Geometry and Hyperbolic Geometry)
• Convex Geometry
• Topology

Algebraic Geometry

This branch of geometry focuses on the zeros of the multivariate polynomial. It consists of linear and polynomial algebraic equations for solving sets of zeros. Applications in this category include string theory and cryptography.

Discrete Geometry

This branch of geometry mainly focuses on the position of simple geometrical objects such as points, lines, triangles, etc. It includes problems based on ordinary continuous spaces that have a combinatorial aspect.

Differential Geometry

It comprises algebraic and calculus techniques for problem-solving. The various problems include problems like general relativity in physics etc.

Euclidean Geometry

In Euclidean geometry, we study planes and solid figures based on axioms and theorems. The fundamental theorems of Euclidean geometry include Points and Lines, Euclid’s Axioms and Postulates, Geometrical Proof, and Euclid’s Fifth Postulate.

There are two types of shapes in Euclidean Geometry: Two dimensional and Three-dimensional shapes. Flat shapes are 2D shapes that include triangles, squares, rectangles, and circles. 3D shapes such as cubes, cuboids, cones, and so on are also known as solids. Fundamental geometry is based on points, lines, and planes, as described in coordinate geometry.

It has multiple applications in the fields of Computer Science, Mathematics, etc.

The five postulates of Euclidean geometry are as follows:

• A straight line can be drawn from one given point to another.
• The length of a straight line is infinite in both directions.
• Any specified point can serve as the circle’s center and any length can serve as the radius.
• All right angles are congruent.
• Any two straight lines that are equal in distance from one another at two points are infinitely parallel.

Some of Euclid’s axioms in geometry that are universally accepted are :

• The things that are equal to the same things are equal. If A = C and B = C then A = C
• If equals are added to equals, the wholes are equal. If A = B and C = D, then A + C = B + D
• If equals are subtracted, the remainders are equal.
• The coinciding things are equal t
• The whole is greater than its part. If A > B, then there exists C such that A = B + C.
• The things that are double the same are equal.
• The things that are halves of the same thing are equal 

Non-Euclidean Geometry

There are two types of Non-Euclidean Geometry- Spherical and Hyperbolic Geometry. It is different from Euclidean geometry due to the difference in the principles of angles and parallel lines. 

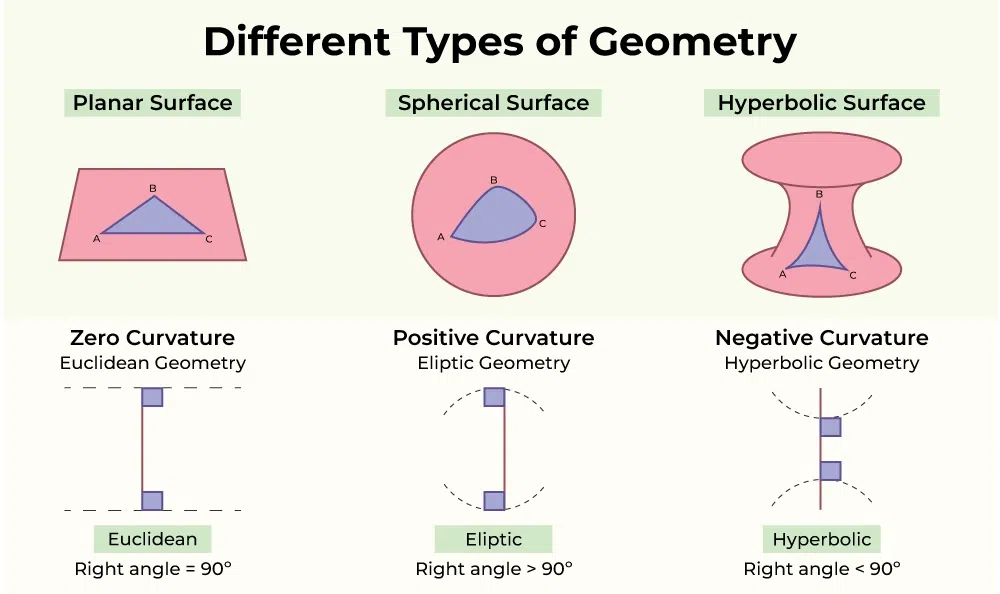
Non-Euclidean Geometry

The study of plane geometry on the sphere is known as spherical geometry. The sum of angles in the triangle is greater than 180°.

A curved surface is referred to as hyperbolic geometry. It is used in Topology.

The planar triangle has a total of angles that is less than 180°, depending on the interior curvature of the curved surface.

Convex Geometry

It consists of convex shapes in Euclidean space and uses techniques that involve real analysis. It is used in various applications of optimization and functional analysis.

Topology 

It comprises the properties of space that are under continuous mapping. It is used in consideration of compactness, completeness, continuity, filters, function spaces, grills, clusters and bunches, hyperspace topologies, initial and final structures, metric spaces, nets, proximal continuity, proximity spaces, separation axioms, and uniform spaces.

Read in Detail: Applications of Topology

Plane Geometry ( 2-D Geometry)

Plane geometry is concerned with the shapes that can be drawn on paper. Euclidean geometry involves the study of plane geometry.

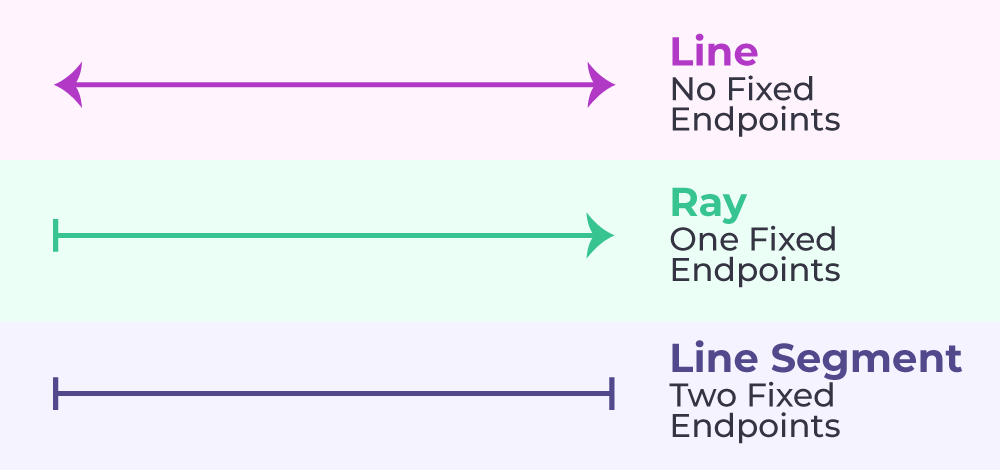
A 2D surface spread infinitely in both directions is referred to as a plane. The basic components of the plane are:

• Points – A point is the no-dimensional fundamental unit of geometry.
• Lines – A line is a straight path on a plane that extends in both directions with no endpoints.
• Angles – Plane geometry consists of lines, circles, and triangles of two dimensions. Plane geometry is another name for two-dimensional geometry. 

Important Points in Plane Geometry

• Collinear points are the ones that lie on the same line.
• A line segment is part of a line that has two endpoints and is finite in length.
• A ray is a line segment that extends indefinitely in one direction. A line has no endpoints.
• Line, line segment, and ray are different from each other.

Plane Geometry

All two-dimensional figures have only two dimensions: length and width. Plane figures consist of squares, triangles, rectangles, circles, and so on. 

Angles in Geometry

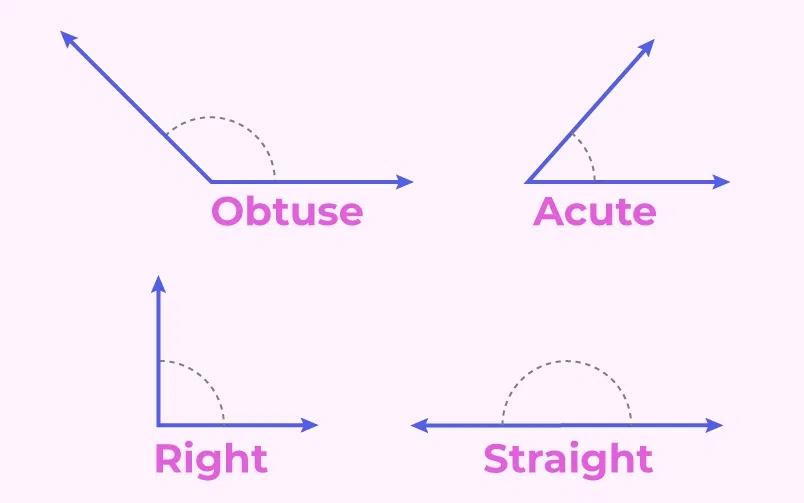
In planar geometry, an angle is formed when two rays intersect, called the sides of the angle, and share a common endpoint known as the vertex of the angle.

There are majorly four types of angles

1. Acute Angle–  An Angle between 0 to 90°.
2. Obtuse Angle– An angle more than 90° but less than 180°.
3. Right Angle– An angle of 90°.
4. Straight Angle– An angle of 180° is a straight line.  

Angles in Geometry

You can find similar topics discussed in depth in the below articles.

1. Lines and Angles
2. Pairs of Angles

Polygon

A figure that is made up of a finite number of straight-line segments closing in a loop. The word ‘poly’ means multiple. 

The sum of internal angles of a polygon is : (n-2) * 180 

where n is the number of sides.

Types of Polygon

The types of polygons are: 

Types of Polygon

Articles Related to Polygons

Here is a list of articles related to Polygons:

1. Polygon
2. Triangles in Geometry
3. Properties of Triangles
4. Types of Quadrilaterals
5. Angle Sum Property of a Quadrilateral
6. Parallelogram
7. Some Special Parallelograms

Geometry is one of the oldest branches of mathematics that is concerned with the shape, size, angles, and dimensions of objects in our day-to-day life. Geometry in

Circle in Geometry

A circle is a closed shape. From a fixed point known as the center, all the points of a circle are of the same distance.

Here is a list of articles where you can find in-depth knowledge about circles.

1. Circle Theorems
2. Lengths of tangents drawn from an external point to a circle are equal
3. Inscribed Shapes in a Circle
4. Cyclic Quadrilateral

Similarity and Congruency in Geometry

Similarity: Two figures are considered similar if they have the same shape or equal angle but may not be necessarily of the same size.

Congruence: Two figures are said to be congruent if they are the same shape and size i.e. they are equal in all means.

Here is a list of articles where you can find in-depth knowledge about the above topic.

1. Construction of Triangles
2. Construction of a Quadrilateral
3. Similar Triangles
4. Pythagoras Theorem and its Converse
5. Thales’s Theorem
6. Criteria for Similarity of Triangles
7. Congruence of Triangles

Solid Geometry

Solid geometry is the study of three-dimensional structures such as cubes, prisms, cylinders, and spheres. 3D figures’ three dimensions are length, width, and height. However, certain solids do not have faces (e.g. sphere).

The analysis of three dimensions in Euclidean space is known as solid geometry. The structures of our environment are three-dimensional.

Both three-dimensional shapes are created by rotating two-dimensional shapes. Essential characteristics of 3D forms are :

• Faces
• Edges
• Vertices

Solid Geometry

Edges 

An edge is the line segment that joins one vertex to another. It helps in forming the outline of 3D shapes. It means it joins one corner point to another. 

Faces

It is defined as the flat surface enclosed by edges that geometric shapes are made up of. It is a 2D figure for all 3D figures. 

Vertices

A vertex is a point where the edges of the solid figure meet each other. It can be referred to as a point where the adjacent sides of a polygon meet. The vertex is the corner where edges meet. 

The number of edges, faces and vertices in different solid shapes is given in the table:

Here is the list of Planar Geometry and Solid Geometry related articles:

1. Visualizing Solid Shapes
2. Faces, Edges and Vertices

Three-Dimensional Geometry

Three-dimensional geometry studies the geometry of shapes in 3D space in the cartesian planes. Every point in the space is referred by 3 coordinates, (x, y, z) that are real numbers.

Here is a list of articles where you can find in-depth knowledge about three-dimensional geometry.

1. Coordinate Geometry
2. GRE Geometry | Three – Dimensional Figures

Geometry Formulas

This are some fundamental geometry formulas:

1. Area Formulas

•     Rectangle: Area = length × width
•     Square: Area = side × side (or side²)
•     Triangle: Area = ½ × base × height
•     Circle: Area = π × radius²

2. Perimeter/Circumference Formulas

•     Rectangle: Perimeter = 2 × (length + width)
•     Square: Perimeter = 4 × side
•     Triangle: Perimeter = side₁ + side₂ + side₃
•     Circle: Circumference = 2 × π × radius

3. Volume Formulas

•     Cube: Volume = side × side × side (or side³)
•     Rectangular Prism: Volume = length × width × height
•     Cylinder: Volume = π × radius² × height
•     Sphere: Volume = ⁴⁄₃ × π × radius³

4. Pythagorean Theorem

    For a right triangle with sides \(a\), \(b\), and hypotenuse \(c\): \(a² + b² = c²\).

5. Trigonometric Ratios (for right triangles):

•     Sine (sin): sin(θ) = opposite / hypotenuse
•     Cosine (cos): cos(θ) = adjacent / hypotenuse
•     Tangent (tan): tan(θ) = opposite / adjacent

These are just a few basic formulas; geometry encompasses a wide range of concepts, each with its own set of formulas and principles.

Read More: Geometry Formulas

Application of Geometry in Real Life

• Imagine standing before a towering skyscraper or walking through a charming bridge. The awe-inspiring shapes and the strength of these structures owe much to geometry, guiding architects and engineers in creating spaces that are not only safe but also pleasing to the eye.
• Art and design are playgrounds for geometric exploration. Artists manipulate shapes and forms to produce stunning visuals, while designers use geometry to bring balance and harmony to everything from sleek websites to cozy living rooms.
• Next time you lose yourself in a video game or a movie’s CGI wonders, remember that geometry is the secret spell behind those captivating visuals. It helps animate characters and build fantastical worlds that seem nearly as tangible as our own.
• The art of cartography, or map-making, transforms the round globe into a flat map with the help of geometry, helping us navigate from point A to point B, whether it’s through bustling city streets or across continents.
• The vastness of space becomes a little more understandable with geometry. It calculates distances to far-off stars and plots the courses of space missions, turning the mysteries of the universe into solvable puzzles.
• In the realm of medicine, geometry’s precise calculations are crucial for technologies like CT scans and MRIs, offering doctors a glimpse inside the human body to diagnose and treat illnesses with remarkable accuracy.
• The convenience of GPS technology, guiding you on your travels or ensuring your online orders arrive at your doorstep, is powered by geometric principles, ensuring accuracy and efficiency in navigation.
• From assembly lines to household helpers, robots rely on geometry to move gracefully and interact with their surroundings, making them indispensable tools in modern manufacturing and daily convenience.
• The next time you dress up or admire a piece of jewelry, consider the geometric principles that influence fashion design, from the symmetry of patterns to the structure of garments.
• Sports aren’t just about physical prowess; they’re also about strategy. Athletes and coaches use geometry to plot game-winning moves, whether it’s the perfect soccer goal or the ideal swim turn.

Geometry Solved Examples

Example 1: If the equal angles measure 50° in an Isosceles triangle then find the third angle.

Solution:

Let the third angle be x

We know that sum of the three angles of a triangle is 180

⇒ x + 50° + 50° = 180°

⇒ x + 100° = 180°

⇒ x = 180° – 100° = 80°

Hence, the third angle measure 80°

Example 2: If one of the angle measure 70° in a parallelogram, find the rest of all the angles.

Solution:

We know that the sum of the adjacent angles of a parallelogram is 180°. Let the angle adjacent to 70° be x

⇒ 70° + x = 180°

⇒ x = 180° – 70° = 110°

We also know that opposite angles of a parallelogram are equal. Hence, the angle opposite 70° will be 70° and the angle opposite 110° will be 110°

Example 3: If a line of length 3 cm is perpendicular to the Chord of the circle 8 cm then find the radius of the circle.

Solution:

We know that a perpendicular from the center to the chord bisects the chord. Hence, the line from the center will touch the midpoint of the chord such that the length of the line on either side measures 4 cm. Now the perpendicular from the center, half of the chord, and the radius will form a right-angled triangle where the radius will be the hypotenuse of the triangle. Hence, the radius of the circle will be given by using the Pythagoras theorem,

r = √3² + 4² = √25 = 5 cm

Example 4: Find the area of the triangle whose base is 24 cm and height is 12 cm.

Solution:

Area of a triangle is given by 1/2 ⨯ base ⨯ height

Here, base = 24 cm, height = 12 cm

Hence, Area of the triangle is 1/2 ⨯ 24 ⨯ 12 = 144cm²

Example 5: Find the area and circumference of a circle whose radius is 7cm.

Solution:

Given that radius = 7 cm

Circumference of a Circle = 2πr = 2 ⨯ 22/7 ⨯ 7 = 44 cm

Area of Circle = πr² = 22/7 ⨯ 7 ⨯ 7 = 154 cm²

People Also Read:

• Triangles in Geometry
• Geometry and Co-ordinates
• Applications of Geometry: Uses in Real-Life

Practice Problems on Geometry

1. Find the area of a rectangle with a length of 8 cm and a width of 5 cm.

2. A parallelogram has sides of 7 cm and 10 cm. Calculate its perimeter.

3. A quadrilateral has three angles measuring 85°, 90°, and 95°. Find the measure of the fourth angle.

4. Calculate the length of a diagonal of a square with side length 6 cm.

5. Find the area of a rhombus with diagonals measuring 10 cm and 24 cm.

6. Determine the measure of one exterior angle of a regular hexagon.

7. Calculate the volume of a cylinder with a radius of 3 cm and a height of 7 cm.

What is Geometry – FAQs

What is Geometry in maths?

Geometry is the branch of mathematics that deals with the shape, size, angles, and dimensions of objects in our day-to-day life.

What are the branches of Geometry?

The geometry can be divided into different parts:

• Algebraic Geometry
• Discrete Geometry
• Differential Geometry
• Euclidean Geometry
• Non Euclidean Geometry(Elliptical Geometry and Hyperbolic Geometry)
• Convex Geometry
• Topology

Why is Geometry important?

Geometry is necessary in our daily life to understand the various shapes and quantify them using area and volume.

What are the basics of Geometry?

The basics of geometry are the proper understanding of points, lines, and planes. It then helps in building all other concepts in geometry that are based on these basic concepts.

What is Euclidean Geometry?

In Euclidean geometry, we study planes and solid figures based on axioms and theorems given by Euclid.

What Is The Difference Between Euclidean and Non-Euclidean Geometry?

Euclidean Geometry is the study of the geometry of flat shapes on a plane, while non-Euclidean geometry is the study of the geometry of curved surfaces.

What are the 2 Types of Geometry?

Plane Geometry and Solid Geometry are the 2 types of Geometry. Plane Geometry is about 2D shapes while Solid Geometry is about 3D shapes.

What are the Basics of Geometry?

The Basics of Geometry are the understanding of Points, Lines, Line Segments, and the types of Geometry.

What are the 8 types of geometry?

1. Euclidean Geometry: Explores plane and solid figures through axioms and theorems.
2. Differential Geometry: Extends calculus principles, crucial in physics for understanding curves and spaces.
3. Algebraic Geometry: Focuses on curves and surfaces, utilizing linear and polynomial algebraic equations.
4. Discrete Geometry: Analyzes relative positions of basic geometric objects.
5. Analytic Geometry: Studies geometric figures and constructions using coordinate systems.
6. Riemannian Geometry: Encompasses non-Euclidean geometries, offering diverse geometric perspectives.
7. Complex Geometry: Investigates geometric structures based on the complex plane.
8. Computational Geometry: Examines properties of explicitly defined algebraic varieties, vital in computational mathematics and computer science.

What is the most common type of geometry?

Euclidean geometry, commonly taught in high schools and featured in pre-collegiate math contests, is the fundamental geometry type. Also referred to as classical geometry, it focuses on the properties of flat, two-dimensional shapes and explores the relationships among points, lines, and angles within a plane.

What is geometry mostly used for?

Geometry is used in many fields, including: Art, Architecture, Engineering, Robotics, Astronomy, Sculptures, Space, Nature, Sports, Machines, Cars.

GeeksforGeeks

Improve