A parallelogram is a two-dimensional geometrical shape whose opposite sides are equal in length and parallel. The opposite angles of a parallelogram are equal in measure and the Sum of adjacent angles of a parallelogram is equal to 180 degrees.
In this article, we will learn about the definition of a parallelogram, its properties, types, theorem, and formulas on its area and perimeter in detail.
What is a Parallelogram?
A parallelogram is defined as a quadrilateral whose two pairs of opposite sides are parallel and equal. The opposite angles of a parallelogram are also equal in measure.
A parallelogram is a four-sided polygon (quadrilateral) and, it has the following key properties:
- Opposite angles are congruent (equal in measure).
- Consecutive angles are supplementary (sum up to 180°).
- Diagonals bisect each other, meaning they cut each other into two equal parts.
- If one of the angles is 90°, it becomes a rectangle. Parallelograms include shapes like rectangles, rhombuses, and squares.
Below is the diagram of a parallelogram ABCD having adjacent sides ‘a’ and ‘b’ and height ‘h’.
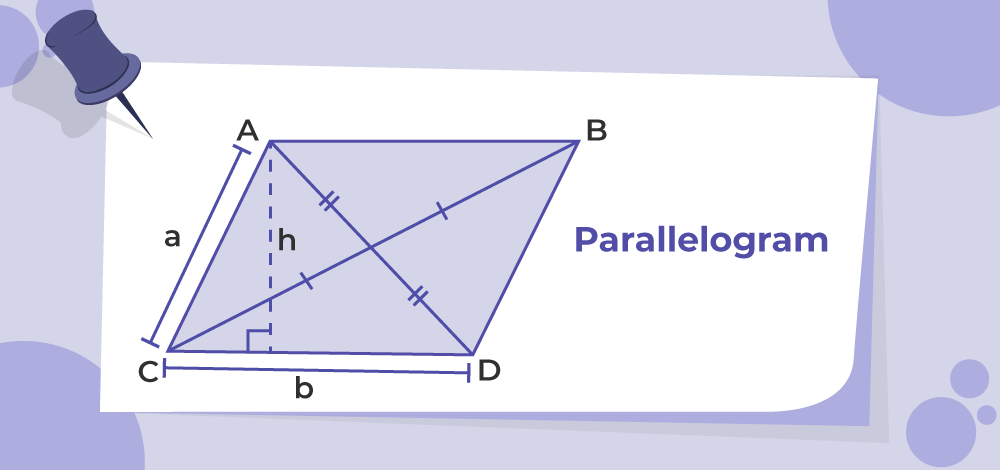
Diagram of a parallelogram
Also Read,
Properties of Parallelogram
The properties of parallelogram are special on its own which are as follows :
- Opposite Sides are Parallel and Equal: The two pairs of opposite sides are both parallel and have equal lengths, i.e., AB = CD and BC = AD.
- Opposite Angles are Congruent: Opposite angles are equal, meaning ∠A = ∠C and ∠B = ∠D.
- Right Angles Form a Rectangle: If one angle is 90°, all angles will be 90°, making it a rectangle.
- Diagonals Bisect Each Other: The diagonals cut each other into two equal halves.
- Consecutive Angles are Supplementary: Any two consecutive angles add up to 180°, i.e., ∠A + ∠B = 180°
Types of Parallelogram
There are mainly four types of parallelogram, based on their properties.
- Rectangle
- Square
- Rhombus
- Rhomboid
Now let’s discuss all these four types of parallelogram in some detail.
Rectangle
A rectangle is a parallelogram with two pairs of equal and parallel opposite sides, along with four right angles.
Observe the rectangle ABCD and associate it with the following properties,
- Two pairs of parallel sides. Here AB || DC and AD || BC
- Four right angles ∠A = ∠B = ∠C = ∠D = 90°.
- The opposite sides are the same length, where AB = DC and AD = BC.
- Two equal diagonals where AC = BD.
- Diagonals that bisect each other.
To learn about rectangles in detail, head over to Rectangle.
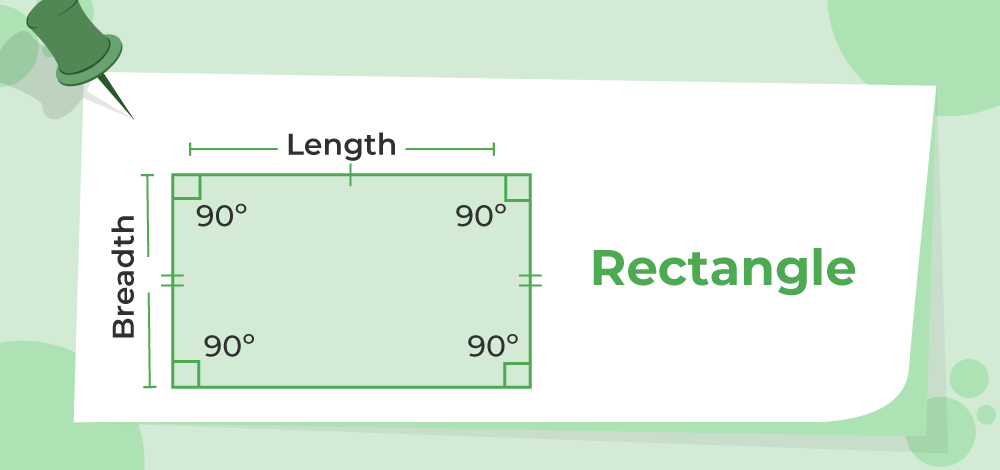
Diagram of a Rectangle
Square
A square is a parallelogram with four equal sides and four equal angles.
Observe the square ACDB and associate it with the following properties:
- Four equal sides are AB = BC = CD = DA.
- Right angles are ∠A = ∠B = ∠C = ∠D = 90°.
- There are two pairs of parallel sides. Here AB || DC and AD || BC.
- Two identical diagonals where AD = BC.
- Diagonals are perpendicular and bisect each other; AD is perpendicular to BC.
To learn about squares in detail, head over to Square.
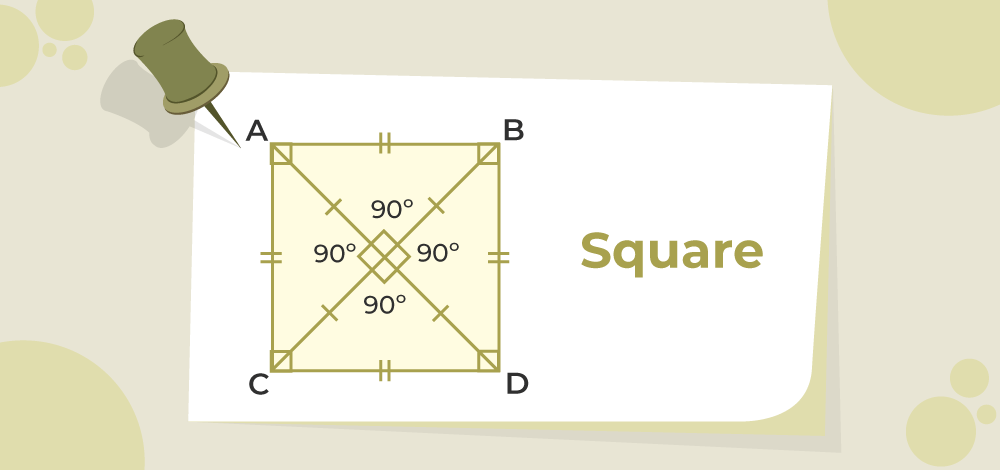
Diagram of a Square
Rhombus
A parallelogram with four equal sides and equal opposite angles is called a rhombus. Consider the diamond ABCD and assign it the following attributes,
- In the given figure, the four equal sides are AB = CD = BC = AD.
- The two pairs of parallel sides are AB || CD and BC || AD.
- The equal opposite angles are ∠A = ∠B and ∠C = ∠D.
- Here, the diagonals (AC and BD) are perpendicular to each other and bisect at right angles.
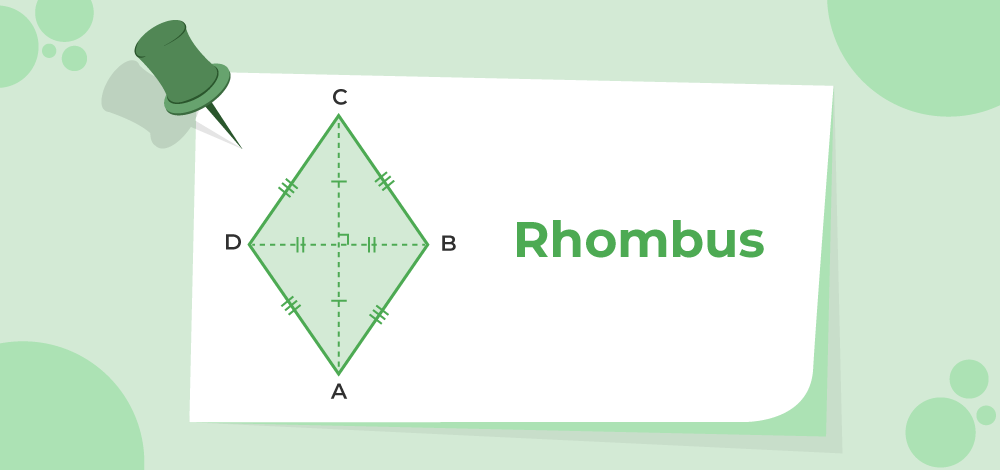
Diagram of a Rhombus
To learn about rhombus in detail, head over to Rhombus.
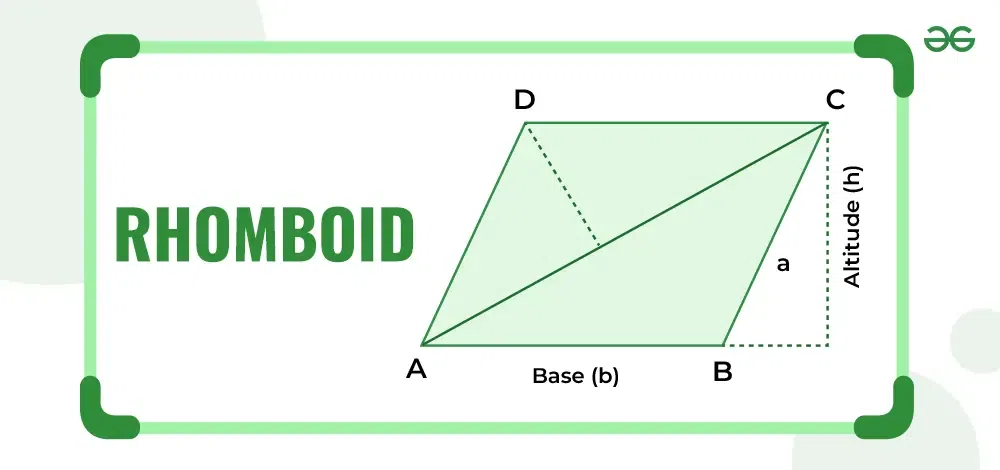
Rhomboid
A rhomboid is a quadrilateral with opposite sides that are parallel and equal in length, but angles are not necessarily right angles. Consider the rhomboid ABCD with the following attributes:
- The equal opposite sides are AB = CD and BC = AD.
- The two pairs of parallel sides are AB ∥ CD and BC ∥ AD.
- The opposite angles are equal: ∠A = ∠C and ∠B = ∠D.
- The diagonals (AC and BD) bisect each other but are not perpendicular.
All 2D shapes have two basic formulas for area and perimeter. Parallelogram is a basic 2-dimensional figure which is widely used in mathematics.
All the formulas on parallelogram can be subdivided into two parts:
Let us discuss these two formulas in detail.
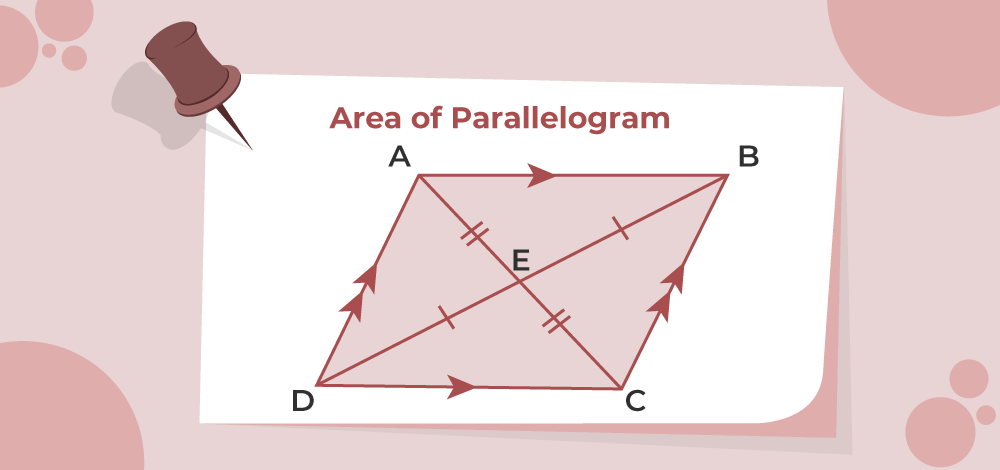
Area of Parallelogram
The area of a parallelogram is the space covered between its four sides.
It can be calculated by knowing the length of the base and the height of the parallelogram and measuring it in square units such as cm2, m2, or inch2. Note the following parallelogram representing the base and height.
Area of a Parallelogram
Consider a parallelogram ABCD with a base (b) and a height (h).
Then, the area of a parallelogram is calculated by the formula:
Area of Parallelogram = base (b) × height (h)
Area of Parallelogram without Height
When the height of the parallelogram is not known, the area can still be found, provided the angle is known to us.
The formula for the area of a parallelogram without height is given as:
Parallelogram area = ab Sinθ
Where a and b are the sides of the parallelogram and θ is the angle between them.
Perimeter of Parallelogram
Perimeter of a parallelogram is the length of its boundary, so it is equal to the sum of all sides.
In a parallelogram, the opposite sides are equal. Let’s say the sides are a and b. Then, the perimeter (P) of the parallelogram with edges is in units of P = 2 (a + b).
Perimeter of Parallelogram = 2 (a + b)
| Property/Formula | Formula/Description |
|---|
| Area (A) | A = b × h |
| Perimeter (P) | P = 2(a + b) |
| Base (b) | Length of the base side. |
| Height (h) | Length of the perpendicular height from base to opposite side. |
| Length of Sides | a,ba, ba,b are the lengths of the adjacent sides. |
| Diagonal Lengths | d1 =
[Tex]\sqrt{a^2 + b^2 + 2ab \cos(\theta)}[/Tex]
d2 =
[Tex]\sqrt{a^2 + b^2 – 2ab \cos(\theta)}[/Tex]
|
| Angles | Opposite angles are equal: ∠A = ∠C
Adjacent angles are supplementary: ∠A + ∠B = 180∘ |
| Relationship Between Sides and Angles | asin(∠B) = bsin(∠A) |
| Area using diagonals |
[Tex]A = \frac{1}{2} \times d_1 \times d_2 \times \sin(\theta)[/Tex]
|
| Circumradius (R) | R =
[Tex]\frac{d_1 \times d_2}{2A}[/Tex]
|
| Inradius (r) | r =
[Tex]\frac{A}{P}[/Tex]
|
Parallelogram Theorem
Let’s understand the theorem on parallelogram and how to prove it.
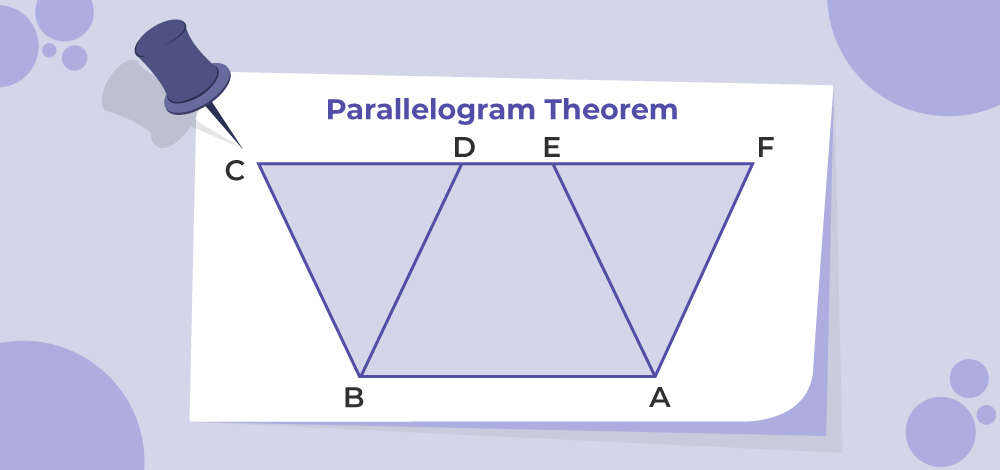
Theorem: Parallelograms on the same base and between the same parallels are equal in area.
To Prove: Area of parallelogram ABCD = Area of parallelogram ABEF
Proof: Let’s assume two parallelograms ABCD and ABEF with the same base DC and between the same parallel lines AB and FC
In the figure given below, the two parallelograms, ABCD and ABEF, lie between the same parallel lines and have the same base. Area ABDE is common between them.
Taking a closer look at the two triangles, △BCD and △AEF might be congruent.
Parallelogram Theorem
BC = AE (Opposite sides of a parallelogram),
∠BCD = ∠AEF (These are corresponding angles because BC || AE and CE are the transversal).
∠BDC = ∠AFE (These are corresponding angles because BD || AF and FD are the transversals).
Thus, by the ASA criterion of congruent triangles. These two triangles are congruent, and they must have equal areas.
area(BCD) = area(AEF)
area(BCD) + area(ABDE) = area(AEF) + area(ABDE)
area(ABCD) = area(ABEF)
Hence, parallelograms lying between the same parallel lines and having a common base have equal areas.
Difference Between Parallelogram and Rectangle
Rectangle and parallelogram are both quadrilaterals. All rectangles are parallelogram as they have all the properties of a parallelogram and more but all parallelograms are not rectangle.
Here we have tabulated some of the basic differences between their properties:
Properties
| Parallelogram
| Rectangle
|
|---|
| Sides | The opposite sides of a parallelogram are equal. | The opposite sides of a rectangle are equal. |
|---|
| Diagonals | The diagonals of a parallelogram bisect each other, but the diagonals are not equal. | The diagonals of a rectangle bisect each other, and the diagonals are equal to each other as well. |
|---|
| Angles | The opposite angles of a parallelogram are equal, and the adjacent angles are supplementary. | All the angles of a rectangle are equal to each other and equal to 90°. |
|---|
Also Check,
Real-Life Examples of a Parallelogram
Various examples of parallelogram as observed in our daily life includes:
- We came across various things in our daily life which resembles a parallelogram such as the computer screen, books, buildings, and tiles all are considered to be in a parallelogram shape.
- The parallelogram is the most common shape which we encounter daily.
- Rectangle and square both can be considered a parallelogram and are easily seen in our daily life.
Solved Examples on Parallelogram
Example 1: Find the length of the other side of a parallelogram with a base of 12 cm and a perimeter of 60 cm.
Solution:
Given perimeter of a parallelogram = 60cm.
Base length of given parallelogram = 12 cm.
P = 2 (a + b) units
Where b = 12cm and P = 40cm.
60 = 2 (a + 12)
60 = 2a + 24
2a = 60-24
2a = 36
a = 18cm
Therefore, the length of the other side of the parallelogram is 18 cm.
Example 2: Find the perimeter of a parallelogram with the base and side lengths of 15cm and 5cm, respectively.
Solution:
Base length of given parallelogram = 15 cm
Side length of given parallelogram = 5 cm
Perimeter of a parallelogram is given by,
P = 2(a + b) units.
Putting the values, we get
P = 2(15 + 5)
P = 2(20)
P = 40 cm
Therefore, the perimeter of a parallelogram will be 40 cm.
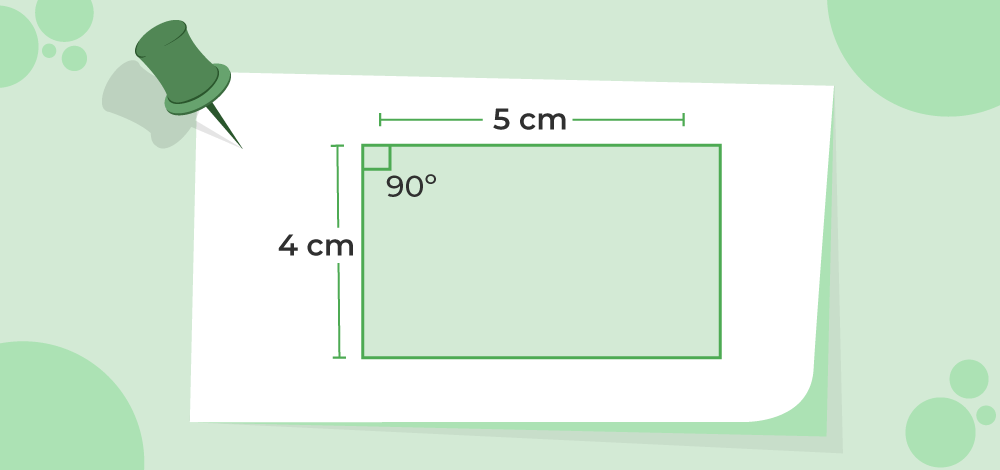
Example 3: The angle between two sides of a parallelogram is 90°. If the lengths of two parallel sides are 5 cm and 4 cm, respectively, find the area.
Solution:
If one angle of the parallelogram is 90°. Then, the rest of the angles are also 90°. Therefore, the parallelogram becomes a rectangle. The area of the rectangle is length times breadth.
Area of parallelogram = 5 × 4
Area of parallelogram = 20cm2
Example 4: Find the area of a parallelogram when the diagonals are given as 8 cm, and 10 cm, the angle between the diagonals is 60°.
Solution:
In order to find the area of the parallelogram, the base and height should be known, lets’s first find the base of the parallelogram, applying the law of cosines,
b2 = 42 + 52 – 2(5)(4)cos(120°)
b2 = 16 + 25 – 40(0.8)
b2 = 9
b = 3cm
Finding the height of the parallelogram,
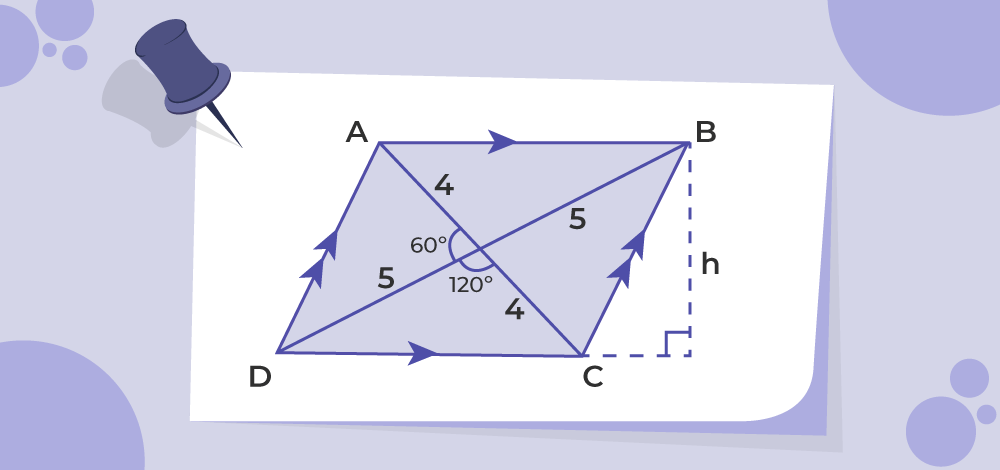
4/sinθ = b/sin120
4/sinθ = 3/-0.58
sinθ = -0.773
θ = 50°
Now, to find the height,
Sinθ = h/10
0.76 = h/10
h = 7.6cm
Area of the parallelogram = 1/2 × 3 × 7.6
= 11.4 cm2
Example 5: Prove that a parallelogram circumscribing a circle is a rhombus.
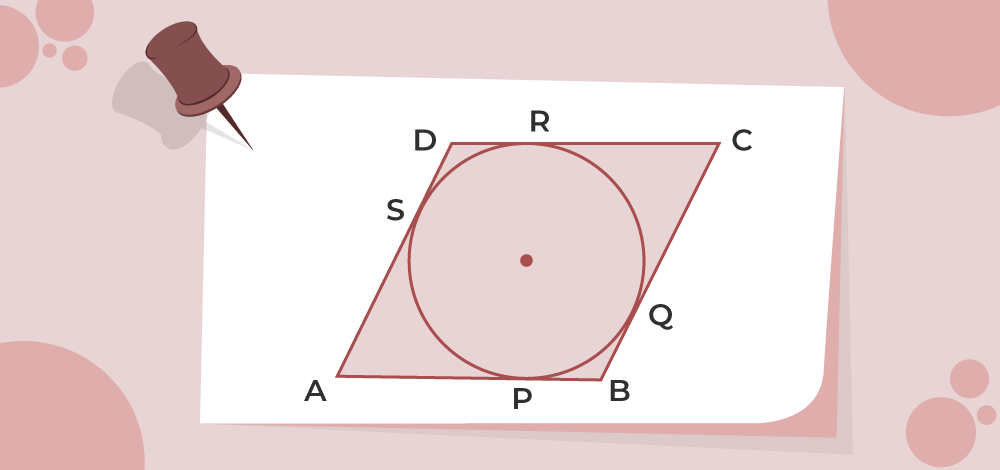
Solution:
Given:
- Parallelogram ABCD
- Circle PQRS
To prove: ABCD is a rhombus.
Proof:
We know that the tangents drawn from an exterior point to a circle are equal to each other. Therefore:
AP = AS ⇢ (1)
BP = BQ ⇢ (2)
DS = DR ⇢ (3)
CR = CQ ⇢ (4)
Adding the LHS and RHS of equations 1, 2, 3, and 4:
AP + BP + DS + CR = AS + BQ + DR + CQ
AB + DR + CR = AS + DS + BC
AB + CD = AD + BC
Since the opposite angles of a parallelogram are equal:
2AB = 2BC
AB = BC, and similarly, CD = AD.
Therefore: AB = CD = BC = AD.
Since all the sides are equal, ABCD is a rhombus.
Practice Problems on Parallelogram
1. In a parallelogram, one angle measures 70°. Find the measure of the remaining angles.
2. If the diagonals of a parallelogram are 16 cm and 30 cm, find the length of the segments formed by each diagonal at the intersection point.
3. In parallelogram ABCD, AB = 8 cm, BC= 5 cm, and the perimeter is 26 cm. Find the lengths of the other two sides.
4. Prove that the diagonals of a parallelogram bisect each other.
5. If the area of a parallelogram is 48 cm² and the base is 8 cm, find the height.
6. A parallelogram has sides 10 cm and 15 cm, and one of its angles is 60°. Find the area of the parallelogram.
7. In parallelogram PQRS, diagonal PR is 12 cm and diagonal QS is 9 cm. Find the length of each segment formed by the diagonals at their intersection.
Parallelograms – FAQs
What is a parallelogram?
A parallelogram is a quadrilateral whose opposite sides are equal in length and parallel to each other. The opposite angles of a parallelogram are equal in measure.
What is the area of a Parallelogram?
The space occupied inside the boundary of the triangle is termed the area of the parallelogram. It can be calculated using the formula,
Area of Parallelogram = Base (b) × Height (h)
What is the Perimeter of a Parallelogram?
The length of all the boundaries of the triangle is termed the perimeter of the parallelogram. It can be calculated using the formula,
Perimeter of Parallelogram = 2(l + b)
Does a parallelogram have equal diagonals?
No, the diagonals of a parallelogram are not equal. However, the diagonals of a parallelogram bisect each other.
How many lines of symmetry parallelogram have?
In general, a parallelogram has 0 lines of symmetry. But in special cases of parallelogram line of symmetry is present. Lines of symmetry of special types of parallelograms are,
| Square | 4 |
| Rhombus | 2 |
| Rectangle | 2 |
Does a parallelogram have equal sides?
Yes, all parallelograms have equal pairs of opposite sides but not all sides are equal in a parallelogram.
Is a rhombus a parallelogram?
Yes, a rhombus is a parallelogram. A rhombus has all the properties of the parallelogram and more.
How is a parallelogram different from a quadrilateral?
All parallelograms are quadrilaterals, but not all quadrilaterals are necessarily parallelograms. For example, a trapezoid is a quadrilateral, not a parallelogram. For a quadrilateral to be a parallelogram, all of its opposite sides must be parallel and equal.
Is a square a parallelogram?
Yes, a square is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a square.
Is a rectangle a parallelogram?
Yes, a rectangle is a parallelogram. Rectangle is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a rectangle.