Maxwell's equations are like the instruction manual for how electricity and magnetism work. They were created by a smart scientist named James Clerk Maxwell in the 1800s. Since these equations help us understand everything from how lights work to how our gadgets and technology function, they are extremely significant. In this article, we'll see Maxwell's Equations in detail, in which there are four equations that forms the description of the topic.
Maxwell’s Equations
Maxwell's equations describe how the electric field can create a magnetic field and vice versa.
Evolution of Maxwell's Equations
Back in the 1800s, people were trying to figure out how electricity and magnetism were connected. Scientists like Michael Faraday and André-Marie Ampère made discoveries that got Maxwell thinking. He put together their ideas and made four special equations that explain how electricity and magnetism are related.
Derivations of Maxwell’s Equations
The four equations of Maxwell's are :
- Maxwell's First Equation (based on Gauss Law)
- Maxwell’s Second Equation (based on Gauss's law on magnetostatics)
- Maxwell’s Third Equation (based on Faraday’s laws of Electromagnetic Induction)
- Maxwell’s Fourth Equation (based on Ampere’s Law)
Maxwell's EquationsGauss’s Law
Gauss law states that “ the net electric flux (ϕc) through any closed surface is equal to the net charge (q) inside the surface divided by ϵ0 ". This describes the nature of the electric field which are around the electric charges. When the charge exist at somewhere then the divergence is non zero ,otherwise it will be zero.
Gauss Law
Mathematically Gauss law can be expressed as:
ϕ_{c} = \frac{q}{ϵ_{0}}
where,
q = net charge enclosed by the gaussian surface
ϵ0 = electric constant
Or, Over a closed surface, the product of the electric flux density vector and surface integral is equal to the charge enclosed.
∯ E.ds = Qenclosed
Maxwell First Equation
Maxwell’s first equation is based on the Gauss law of electrostatic. This law states that "in a closed surface the integral of the electric flux density is equal to the charge enclosed ." The expression for Maxwell’s first equation can be expressed mathematically as,
▽. Edv=ρv
Derivation for Maxwell First Equation:
From the definition of Gauss Law, we have obtained,
∯ E.ds = Qenclosed —–--(1)
As we know that any system is made up of composition of various surfaces but the volume of the system remains consistent. Thus for the convenience in calculation, let’s convert surface integral to volume integral by taking the Divergence of the same vector .
∯ E.ds = ∭ ▽. Edv ----(2)
On combining equation (1) and (2) we obtain,
∭▽. Edv = Qenclosed —–--(3)
when we supply some amount of charges to the system, it will spread throughout its volume. Thus volume charge density (that is number of charges per unit volume) of the system can be expressed as
pv = \frac{dQ}{dv}
or, dQ=pvdv —–--(4)
Total charges enclosed can be obtained by integrating equation (3) i.e ,
Q=∭ρvdv —–--(5)
On Substituting the value of Q obtained in equation (5) to equation (3), we get,
∭▽. Edv = ∭ρvdv
Therefore, ⇒ ▽. Edv = ρvdv
This is the required expression for Maxwell’s First equation. This equation is also referred to as Gauss’s law of Electrostatic.
Gauss’s Law for Magnetism
Gauss law on magnetostatics states that “closed surface integral of magnetic flux density is always equal to total scalar magnetic flux enclosed within that surface of any shape or size lying in any medium.”
Gauss's Law for Magnetism
Mathematically it is expressed as:
∯ B.ds =ϕenclosed
Maxwell’s Second Equation
Maxwell second equation is based on Gauss law on magnetostatics. This law states that " the sum of outer flux in the magnetic induction through any closed surface is zero". The expression for Maxwell’s first equation can be expressed mathematically as:
▽. H = 0
Derivation for Maxwell’s Second Equation
According to Gauss law on magnetostatics
∯ B . ds = ϕenclosed —–--(1)
Magnetic flux cannot be enclosed inside a surface
∯ B . ds = 0 —–--(2)
Converting surface integral to a volume integral using divergence of vectors
∯ B . ds = ∭ Δ . Bdv —–--(3)
On substituting (3) in (2) we get,
∭ Δ . Bdv = 0 —–--(4)
The above equation can be satisfied using only the following two conditions:
However, the volume of an object cannot be 0, thus Δ . B = 0
where, B = μH is the flux density.
Therefore,
Δ . H = 0 is the required expression.
Faraday's Laws of Electromagnetic Induction
Faraday's law states that “Whenever there is a change of magnetic flux in a circuit, an induced electromotive force or emf is produced. The emf lasts only for the time for which the flux is changing''.
Faraday's Laws of Electromagnetic Induction
Mathematically Alternating emf is expressed as:
emf _{alt} = - N \frac{dϕ}{dt}
where,
N is the number of turns in a coil.
ϕ is the scalar magnetic flux.
The negative sign indicates that the induced emf always opposes the time-varying magnetic flux.
Maxwell’s Third Equation
Maxwell’s 3rd equation is derived from Faraday’s laws of Electromagnetic Induction, which states that " the line integral of magnetic field in a closed circuit is equal to the closed current." The expression for Maxwell’s first equation can be expressed mathematically as:
▽× E = - \frac{δB}{ δt}
Derivation for Maxwell’s Third Equation
According to Faraday's law ,
emf _{alt} = -\frac{d ϕ }{ dt}
—–--(1)
Total magnetic flux on arbitrary surface S is
ϕ = ∬ B.ds
Substitute the value of magnetic flux in equation (1), we get,
emf _{alt} = − \frac{(d∬B.ds)}{dt}
emf_{alt} = ∬ − ( \frac{δB}{dt} ).ds
—–--(2)
Since, the induced alternative emf in the coil is basically a closed path, thus it can be expressed mathematically as closed integral as,
emfalt = ∮ E . dl —–--(3)
From equation (2) and (3)
∮ E . dl = ∬ − ( \frac{δB}{dt}
).ds —–--(4)
By using stroke's Theorem contour integration can be converted to surface integration as
∮ E . dl = ∬ (▽× E ) .ds
By substituting this value in equation (4) we get,
∬ ( ▽× E ) ds = ∬ − ( \frac{δB}{dt}
).ds
Therefore , ▽× E = - ( \frac{δB}{dt}
) is the required equation.
This equation is Faraday’s law of electromagnetic induction.
Ampere's Law
According to Ampere's law, the magnetic field line integral around a closed path is equal to the product of the magnetic permeability of that space and the total current through the area bounded by that path.
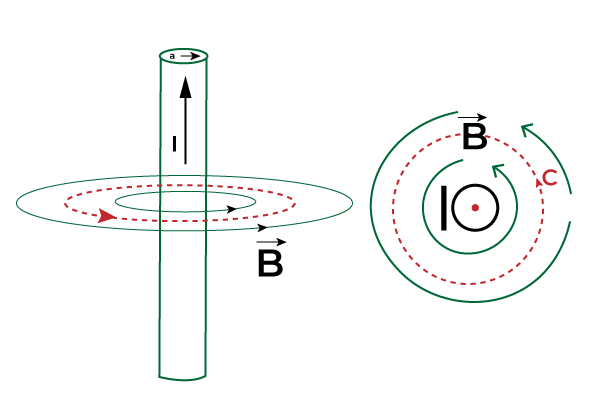Ampere's LawMathematically we can express it as:
∮ Bdl = μ0I
Maxwell’s Fourth Equation
Maxwell’s fourth equation is derived from Ampere’s Law, which states that "the magnetic field divergence is always zero." The expression for Maxwell’s first equation can be expressed mathematically as:
▽× H = J + (\frac{∂D}{ ∂t} )
Derivation for Maxwell’s fourth Equation
According to Ampere's circuital law
∮ B.dl = μ0i ----- (1)
According to Stoke's theorem-
∮ B.dl = ∮S ( ∇ × B ).ds ----- (2)
From equation (1) and equation(2)
∮S ( ∇ × B ).ds = μ0i ----- (3)
where i = ∮S J . ds ----- (4)
So from equation (3) and equation (4)
∮S ( ∇ × B ) .ds = μ0 ∮S (J . ds )
∮S ( ∇ × B ) .ds - μ0 ∮S (J . ds ) = 0
∮S [ ( ∇ × B ) - μ0 J ] .ds = 0
( ∇ × B ) − μ0 J = 0
( ∇ × B ) = μ0 J
As we know that B = μ0 H
∇ × H = J
Modified Maxwell's Fourth Equation
The modified Maxwell's fourth equation is the differential form of the modified Ampere's circuital law.
We know the modified Ampere's circuital law-
∮ B . dl = μ0 i + id
Where id = Displacement current
Therefore the modified Maxwell's fourth equation can be written as-
∇ × H = J + Jd ----- (1)
Where Jd = Displacement current density
And its value of Jd is :
Jd = ϵ0 (∂E/∂t)
and
Jd = ∂D/∂t ( ∵ D = ϵ0E)
Now substitute the value of Jd in equation (1)
Therefore , ▽× H = J + (∂D / ∂t ) .
This is the required equation
Application of Maxwell's Equation
There are many application and uses of Maxwell’s equations in the field of electrodynamics.
- The equations act as a mathematical model for electric, optical, and radio technologies such as power production, electric motors, wireless communication, lenses, radar, and so on.
- They describe how charges, currents, and field changes produce electric and magnetic fields.
- According to Maxwell's equations, a changing magnetic field always produces an electric field, and a changing electric field always induces a magnetic field.
Advantages and Disadvantages of Maxwell's Equation
There are some list of Advantages and Disadvantages of Maxwell's Equation given below :
Advantages of Maxwell's Equation
- Maxwell's equations shows the connection between the theory of magnetism and electricity.
- Various electromagnetic phenomena like the propagation of electromagnetic waves, including light, behaviour of electric circuits were predicted and explained by Maxwell's equations .
- These equations are the foundation for classical electrodynamics. They are necessary to comprehend how electromagnetic fields are produced by charges and currents.
- The emergence of light as an electromagnetic wave, gave a way for the development of technologies like radio, television, and wireless communication, was made possible by Maxwell's equations, which predicted electromagnetic waves.
- Modern physics rely on Maxwell's equations, which have influenced development of other theories including quantum mechanics and special relativity.
Disadvantages of Maxwell's Equation
- Although Maxwell's equations are based on the principles of classical electrodynamics, more sophisticated theories are required when applying them to very tiny scales (quantum electrodynamics) and very high speeds (relativistic electrodynamics).
- Maxwell's equations do not account for quantum effects.
- Certain presumptions and simplifications, such as the lack of magnetic monopoles and the idealized characteristics of materials, form the foundation of Maxwell's equations. These presumptions might not always adequately represent occurrences that occur in the real world.
- Maxwell's equations are simple, but solving them for complicated geometries and boundary conditions can be challenging.
- Concepts of gravitational force quantum mechanics are not included in Maxwell's equations, which constitute a classical theory.
Conclusion
In this article we have learned about Maxwell's equations, evolution, and applications. Maxwell's equations represent a remarkable achievement in the history of science. They have provided a unifying framework for understanding electricity and magnetism, giving rise to groundbreaking technological advancements and revolutionizing the way we perceive the physical world.
FAQs on Maxwell's Equation
What is the importance of Maxwell equations?
A very important consequence of the Maxwell equations is that these can be used to derive the law of conservation of charges. Essentially it provides a description about the behavior of electromagnetic radiation in the general medium.
What is meant by scalar electric flux?
Scalar electric flux are the imaginary lines of force radiating in an outward direction.
What is meant by scalar magnetic flux?
They are the circular magnetic field generated around a current-carrying conductor.
Similar Reads
Maxwell's Equation
Maxwell's equations are like the instruction manual for how electricity and magnetism work. They were created by a smart scientist named James Clerk Maxwell in the 1800s. Since these equations help us understand everything from how lights work to how our gadgets and technology function, they are ext
10 min read
Pedal Equation
Pedal Equation is a fascinating concept in geometry that relates a specific point on a curve to its tangent lines. In simple terms, the pedal equation describes the relationship between two key distances: the distance from a fixed point (known as the pedal point) to any point on a curve, and the per
8 min read
Nernst Equation
Electrochemistry is the study of the relationship between electrical energy and chemical reactions. It deals with the transfer of electrons between substances and their chemical reactions. This subject provides the basis for understanding the behaviour of batteries, fuel cells, and other types of en
8 min read
Van Der Waals Equation
Van der Waals equation is an equation of state that describes the behavior of real gases, taking into account the finite size of gas molecules and the attractive forces between them. Van Der Waals equation is written like this: [P + a (n2/V2)] (V-nb) = nRT. The Van der Waals equation stands as a cru
12 min read
Maxwell's Equations in Electromagnetism
Maxwell's Equations are a set of four equations proposed by mathematician and physicist James Clerk Maxwell in 1861 to demonstrate that the electric and magnetic fields are co-dependent and two distinct parts of the same phenomenon known as electromagnetism. These formulas show how variations in the
12 min read
Mirror Equation
Mirror Equation in Physics is the equation for mirrors that provides the relation between the distance of the object and the image, as well as its focal length. Mirror Equation is helpful in determining object position, image position or focal length given that two of the parameters are given. In op
11 min read
Solving Exponential Equations
Exponential equations are equations where the variable appears as an exponent. Solving these equations involves various techniques depending on the structure of the equation. A common method is rewriting both sides of the equation with the same base and then equating the exponents. However, if the b
5 min read
Reciprocal Equation
A reciprocal equation is an equation which can be represented in the form of 1/x or x-1. Reciprocal equations have many real-life applications in various fields such as engineering, wave, optics, etc. In this article, we will learn about reciprocal equations, different types of reciprocal equations,
9 min read
Equation of a Sphere
The equation of a sphere defines all points equidistant from its center, given by (x - h)² + (y - k)² + (z - l)² = r², where (h, k, l) is the center and r is the radius. This article provides an in-depth exploration of the equation of a sphere, its properties, applications, and related concepts. Tab
8 min read
Parametric Equations
Parametric equations are a way to describe curves and shapes using one or more parameters. Instead of expressing coordinates directly, we use these parameters to define how points move along the curve. This method offers flexibility in representing complex curves and analyzing their behaviour, makin
9 min read
Exponential Equation Formula
Exponents are used in exponential equations, as the name implies. The exponent of a number (base) indicates how many times the number (base) has been multiplied. An exponential equation is one in which the power is a variable and is a part of an equation. Exponential EquationsA variable is the expon
3 min read
Linear Equations Formula
A linear equation is known as the algebraic equation that represents the straight line. It is composed of variables and constants. Linear equations consist of the first-order, that involves the highest power to any of the involved variables i.e. It is also considered as the polynomial of a degreeThe
8 min read
Equations with Variables
An equation in algebra consist of two algebraic expressions separated by an inequality sign generally equal to. For example, ax + b = c. These equations consist of some numbers, a variable, operator sign and inequality sign. An equation with variable is used to represent a general condition . For ex
7 min read
Cauchy Euler Equation
Cauchy-Euler equation, also known as the Euler-Cauchy equation, is a type of linear differential equation with variable coefficients. It has the general form [Tex] x^n y^{(n)} + a_{n-1} x^{n-1} y^{(n-1)} + \cdots + a_1 x y' + a_0 y = 0[/Tex]. It's named after two famous mathematicians, Cauchy and Eu
6 min read
Expressions And Equations
Expression and Equations are two important concepts of algebra in mathematics. We need to learn about expressions and equations to solve different types of easy and complex problems in both mathematics and real-life applications. expression is a combination of numbers, variables, and operators while
7 min read
Telegrapher's Equation
In the world of wireless Communication, the Telegraph Equation is a vastly talked about concept in the study of transmission lines, particularly in Electrical engineering and telecommunications. Much specifically, for high-frequency transmission lines, It precisely describes the propagation of elect
13 min read
Maxwell–Boltzmann Distribution
From the kinetic theory of gases, we have learnt that all the particles in air travel at different speeds and the speed of each particle are due to the collisions between the particles present in the air. Thus, we cannot tell the speed of each particle in the gas or air. Instead, we can tell the num
7 min read
Cauchy-Riemann Equations
Cauchy-Riemann equations are fundamental in complex analysis, providing essential conditions for a function of a complex variable to be complex differentiable, or analytic. Named after Augustin-Louis Cauchy and Bernhard Riemann, these equations connect the partial derivatives of the real and imagina
14 min read
Derivation of Ideal Gas Equation
The ideal gas law is a well-defined approximation of the behaviour of several gases under various situations in thermodynamics. The Ideal Gas Equation is a mathematical formula that uses a combination of empirical and physical constants to express the states of hypothetical gases. The general gas eq
9 min read
Einstein's Photoelectric Equation
Albert Einstein published an equation to explain this effect in 1905, the annus mirabilis (wonder year) of Physics. Light, according to Einstein, is a wave that interacts with matter as a packet of energy or a quantum of energy. The photon was the quantum of radiation, and the equation was known as
9 min read