Pascal’s Triangle Formula

Probability is the backbone of mathematics. It tells how an event is likely to occur. It deals with the numerical justification of making more probable decisions. Higher the probability, more chances of an event occurring and vice-versa. Pascal’s triangle is a beautiful concept of probability developed by the famous mathematician Blaise Pascal which is used to find coefficients in the expansion of any binomial expression.

Pascal Triangle 

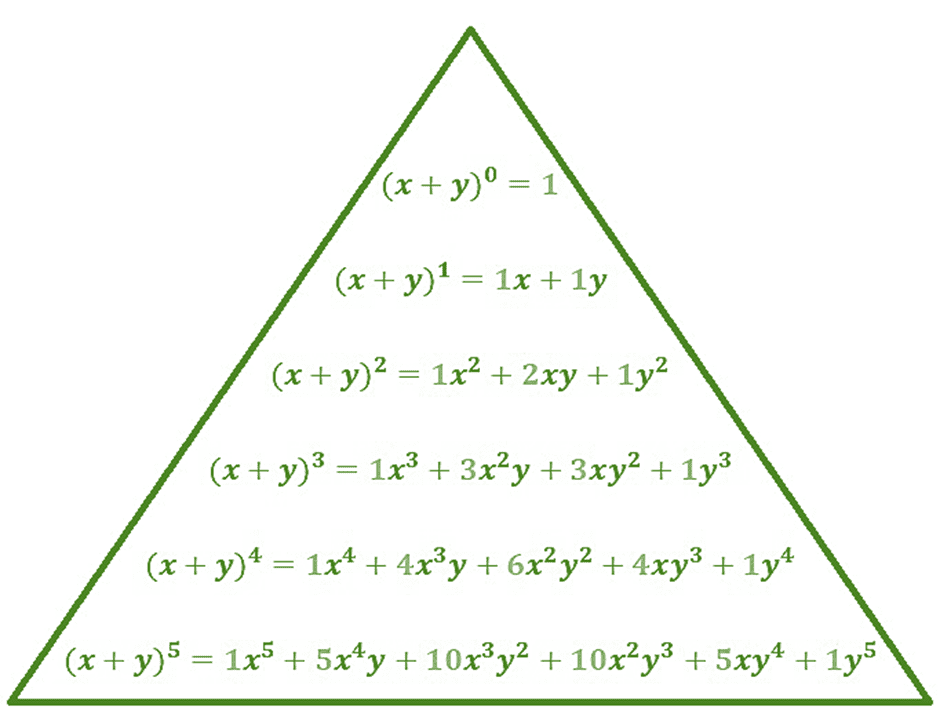
Pascal’s Triangle is a method to know the binomial coefficients of terms of binomial expression (x + y)ⁿ, where n can be any positive integer and x,y are real numbers. Pascal Triangle is represented in a triangular form, it is kind of a number pattern in the form of a triangular arrangement. It begins with 1 on the top and with 1 running down on the two sides of the triangle. In the pascal triangle, each new number between two numbers and below then and its value is the sum of two numbers above. This triangle is used in different types of probability conditions. Here each row represents the coefficient of expansion of (x + y)ⁿ.

Zero row n = 0, (x + y)⁰

First row n = 1 , (x + y)¹ 

Second row n = 2, (x + y)² 

Third row n = 3, (x + y)³

Fourth row n = 4, (x + y)⁴ 

Here the power of y in any expansion of (x + y)ⁿ represents the column of Pascal’s Triangle. n represents the row of Pascal’s triangle. Row and column are 0 indexed in Pascal’s Triangle.

Pascal’s Triangle Construction

It’s quite simple to make a pascal triangle. Start from the top row (0th row) by writing just number 1. In the corresponding rows, the new square in the pascal triangle is going to be the sum of squares directly above this square and touching it. For example, finding the sum of square row 4 and column 2 is the sum of the square of row 3 column 1 and row 3 column 2. So the square of row 4 column 2 has a value 1 + 2 = 3.

Properties of Pascal’s Triangle

1. Each number in Pascal’s Triangle is the sum of two numbers above it.
2. Numbers in a row are symmetric in nature.
3. Each number represents a binomial coefficient.
4. Numbers on the left and right sides of the triangle are always 1.
5. nth row contains (n+1) numbers in it.

Pascal’s Triangle Formula

The pascal’s triangle formula to find the elements in the nth row and kth column of the triangle is 

[Tex]p \choose q   [/Tex]=  {p-1} \choose {q-1} {p-1} \choose {q-1}[Tex] {p-1} \choose {q-1}  [/Tex] + [Tex] {p-1} \choose {q}[/Tex]

Here, 0 ≤ q ≤ p, p is a non-negative number

Or the formula to find number in the nth row and rth column is given by ^pC_q = p!/(p – q)!q!

^pC_q =^pC_q-1 + ^p-1C_q-1 

Pascal’s Triangle Binomial Expansion

As we already know that pascal’s triangle defines the binomial coefficients of terms of binomial expression (x + y)ⁿ, So the expansion of (x + y)ⁿ is:

(x + y)ⁿ = a₀xⁿ + a₁x^n-1 + ……a_n-1xy^n-1 + a_nyⁿ

Sample Questions

Question 1: Find the coefficient of the term x^2y in the expansion of (x + y)³.

Solution:

Method 1:

We look at the row 3rd row of Pascal’s Triangle because n is 3 and 1st column of the Pascal’s Triangle because power of y is 1 in the term x^2y. So the coefficient is 3.

Method 2:

We simply apply ⁿC_r where n = 3, r = 1.

So coefficient of x^2y in the expansion of (x + y)³ is ³C₁ = 3

Question 2: Find the coefficient of the term x²y² in the expansion of (4x + 3y)⁴.

Solution:

Method 1:

We look at the row 4th row of Pascal’s Triangle because n is 4 and 2nd column of the Pascal’s Triangle because power of y is 2 in the term x²y². So number in Pascal’s Triangle is 6. 

But we see that coefficient of x is 4 and y is 3 now since power of x is 2 and y is 2 in the term x²y² so pascal Triangle number will be multiplied by 4² and 3² to find the coefficient.

Coefficient = 6 x 4² x 3² = 864

Method 2:

We simply apply ⁿC_r where n = 4, r = 2.

So Pascal Triangle number of term x²y² in the expansion of (4x +3y)⁴ is ⁴C₂ = 6.

But we see that coefficient of x is 4 and y is 3 now since power of x is 2 and y is 2 in the term x²y² so pascal Triangle number will be multiplied by 4² and 3² to find the coefficient.

Coefficient = 6 x 4² x 3² = 864

Question 3: Write the 6th row of the Pascal’s Triangle

Solution:

6th row can be written as :  6C0 6C1 6C2 6C3 6C4 6C5 6C6

                                               1, 6, 15, 20, 15, 6, 1

Question 4: Find the coefficient of the term x⁴ in the expansion of (2x + y)⁴.

Solution:

Method 1:

We look at the row 4th row of Pascal’s Triangle because n is 4 and 0th column of the Pascal’s Triangle because power of y is 0 in the term x⁴. So number in Pascal’s Triangle is 1.

But we see that coefficient of x is 2 and y is 0 now since power of x is 4 and y is 0 in the term x⁴ so Pascal Triangle’s number will be multiplied by 2⁴ and 1⁰ to find the coefficient.

Coefficient = 1 x 2⁴ x 1⁰= 16 

Method 2:

We simply apply ⁿC_r where n = 4, r = 0.

So Pascal Triangle number of term x⁴ in the expansion of (2x + y)⁴ is ⁴C₀ = 1.

But we see that coefficient of x is 2 and y is 0 now since power of x is 4 and y is 0 in the term x⁴ so Pascal Triangle’s number will be multiplied by 2⁴ and 1⁰ to find the coefficient.

Coefficient = 1

Question 5: Find the coefficient of the term xy² in the expansion of (2x + y)³.

Solution:

Method 1:

We look at the row 3rd row of Pascal’s Triangle because n is 3 and 2nd column of the Pascal’s Triangle because power of y is 2 in the term xy². So number in Pascal’s Triangle is 3.

But we see that coefficient of x is 2 and y is 1 now since power of x is 2 and y is 1 in the term xy² so Pascal Triangle’s number will be multiplied by 2¹ and 1² to find the coefficient.

Coefficient = 3 x 2¹ x 1² = 6  

Method 2:

We simply apply ⁿC_r where n = 3, r = 2.

So Pascal Triangle number of term xy² in the expansion of (2x + y)³ is ³C₂ = 3.

But we see that coefficient of x is 2 and y is 1 now since power of x is 2 and y is 1 in the term xy^2 so Pascal Triangle’s number will be multiplied by 2¹ and 1² to find the coefficient.

Coefficient = 3 x 2¹ x 1² = 6  

S

siddharthkalra2002

Follow

Improve

Article Tags :

• Mathematics
• School Learning
• Math-Concepts
• Maths-Formulas