Total number of possible Binary Search Trees and Binary Trees with n keys

Last Updated : 30 Dec, 2022

Total number of possible Binary Search Trees with n different keys (countBST(n)) = Catalan number Cn = (2n)! / ((n + 1)! * n!)

For n = 0, 1, 2, 3, … values of Catalan numbers are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …. So are numbers of Binary Search Trees.

Total number of possible Binary Trees with n different keys (countBT(n)) = countBST(n) * n!

Below is code for finding count of BSTs and Binary Trees with n numbers. The code to find n’th Catalan number is taken from here.

C++

// See https://www.geeksforgeeks.org/program-nth-catalan-number/
// for reference of below code.
 
#include <bits/stdc++.h>
using namespace std;
 
// A function to find factorial of a given number
unsigned long int factorial(unsigned int n)
{
    unsigned long int res = 1;
 
    // Calculate value of [1*(2)*---*(n-k+1)] / [k*(k-1)*---*1]
    for (int i = 1; i <= n; ++i)
    {
        res *= i;
    }
 
    return res;
}
 
unsigned long int binomialCoeff(unsigned int n, unsigned int k)
{
    unsigned long int res = 1;
 
    // Since C(n, k) = C(n, n-k)
    if (k > n - k)
        k = n - k;
 
    // Calculate value of [n*(n-1)*---*(n-k+1)] / [k*(k-1)*---*1]
    for (int i = 0; i < k; ++i)
    {
        res *= (n - i);
        res /= (i + 1);
    }
 
    return res;
}
 
 
// A Binomial coefficient based function to find nth catalan
// number in O(n) time
unsigned long int catalan(unsigned int n)
{
    // Calculate value of 2nCn
    unsigned long int c = binomialCoeff(2*n, n);
 
    // return 2nCn/(n+1)
    return c/(n+1);
}
 
// A function to count number of BST with n nodes 
// using catalan
unsigned long int countBST(unsigned int n)
{
    // find nth catalan number
    unsigned long int count = catalan(n);
 
    // return nth catalan number
    return count;
}
 
// A function to count number of binary trees with n nodes 
unsigned long int countBT(unsigned int n)
{
    // find count of BST with n numbers
    unsigned long int count = catalan(n);
 
    // return count * n!
    return count * factorial(n);
}
 
// Driver Program to test above functions
int main()
{
 
    int count1,count2, n = 5;
 
    // find count of BST and binary trees with n nodes
        count1 = countBST(n);
        count2 = countBT(n); 
     
    // print count of BST and binary trees with n nodes
    cout<<"Count of BST with "<<n<<" nodes is "<<count1<<endl;
        cout<<"Count of binary trees with "<<n<<" nodes is "<<count2;
 
    return 0;
}

Java

// See https://www.geeksforgeeks.org/program-nth-catalan-number/
// for reference of below code.
import java.io.*;
 
class GFG 
{
     
// A function to find 
// factorial of a given number
static int factorial(int n)
{
    int res = 1;
 
    // Calculate value of 
    // [1*(2)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for (int i = 1; i <= n; ++i)
    {
        res *= i;
    }
 
    return res;
}
 
static int binomialCoeff(int n,
                         int k)
{
    int res = 1;
 
    // Since C(n, k) = C(n, n-k)
    if (k > n - k)
        k = n - k;
 
    // Calculate value of 
    // [n*(n-1)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for (int i = 0; i < k; ++i)
    {
        res *= (n - i);
        res /= (i + 1);
    }
 
    return res;
}
 
 
// A Binomial coefficient 
// based function to find 
// nth catalan number in 
// O(n) time
static int catalan( int n)
{
     
    // Calculate value of 2nCn
    int c = binomialCoeff(2 * n, n);
 
    // return 2nCn/(n+1)
    return c / (n + 1);
}
 
// A function to count number of
// BST with n nodes using catalan
static int countBST( int n)
{
    // find nth catalan number
    int count = catalan(n);
 
    // return nth catalan number
    return count;
}
 
// A function to count number
// of binary trees with n nodes 
static int countBT(int n)
{
    // find count of BST
    // with n numbers
    int count = catalan(n);
 
    // return count * n!
    return count * factorial(n);
}
 
// Driver Code
public static void main (String[] args)
{
    int count1, count2, n = 5;
 
    // find count of BST and 
    // binary trees with n nodes
    count1 = countBST(n);
    count2 = countBT(n); 
 
    // print count of BST and 
    // binary trees with n nodes
    System.out.println("Count of BST with "+ 
                            n +" nodes is "+ 
                                    count1);
    System.out.println("Count of binary " + 
                             "trees with "+ 
                         n + " nodes is " + 
                                   count2);
}
}
 
// This code is contributed by ajit

Python3

# See https:#www.geeksforgeeks.org/program-nth-catalan-number/ 
# for reference of below code. 
 
# A function to find factorial of a given number 
def factorial(n) :
    res = 1
     
    # Calculate value of [1*(2)*---*
    #(n-k+1)] / [k*(k-1)*---*1] 
    for i in range(1, n + 1): 
        res *= i 
    return res 
 
def binomialCoeff(n, k): 
 
    res = 1
 
    # Since C(n, k) = C(n, n-k) 
    if (k > n - k): 
        k = n - k 
 
    # Calculate value of [n*(n-1)*---*(n-k+1)] / 
    # [k*(k-1)*---*1] 
    for i in range(k): 
     
        res *= (n - i) 
        res //= (i + 1) 
     
    return res 
 
# A Binomial coefficient based function to 
# find nth catalan number in O(n) time 
def catalan(n):
 
    # Calculate value of 2nCn 
    c = binomialCoeff(2 * n, n) 
 
    # return 2nCn/(n+1) 
    return c // (n + 1) 
 
# A function to count number of BST 
# with n nodes using catalan 
def countBST(n):
 
    # find nth catalan number 
    count = catalan(n) 
 
    # return nth catalan number 
    return count 
 
# A function to count number of binary 
# trees with n nodes 
def countBT(n):
 
    # find count of BST with n numbers 
    count = catalan(n) 
 
    # return count * n! 
    return count * factorial(n) 
 
# Driver Code 
if __name__ == '__main__':
 
    n = 5
 
    # find count of BST and binary
    # trees with n nodes 
    count1 = countBST(n) 
    count2 = countBT(n) 
 
    # print count of BST and binary trees with n nodes 
    print("Count of BST with", n, "nodes is", count1) 
    print("Count of binary trees with", n, 
                       "nodes is", count2)
 
# This code is contributed by
# Shubham Singh(SHUBHAMSINGH10)

C#

// See https://www.geeksforgeeks.org/program-nth-catalan-number/
// for reference of below code.
using System;
 
class GFG
{
     
// A function to find 
// factorial of a given number
static int factorial(int n)
{
    int res = 1;
 
    // Calculate value of 
    // [1*(2)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for (int i = 1; i <= n; ++i)
    {
        res *= i;
    }
 
    return res;
}
 
static int binomialCoeff(int n,
                         int k)
{
    int res = 1;
 
    // Since C(n, k) = C(n, n-k)
    if (k > n - k)
        k = n - k;
 
    // Calculate value of 
    // [n*(n-1)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for (int i = 0; i < k; ++i)
    {
        res *= (n - i);
        res /= (i + 1);
    }
 
    return res;
}
 
// A Binomial coefficient 
// based function to find 
// nth catalan number in 
// O(n) time
static int catalan(int n)
{
     
    // Calculate value
    // of 2nCn
    int c = binomialCoeff(2 * n, n);
 
    // return 2nCn/(n+1)
    return c / (n + 1);
}
 
// A function to count 
// number of BST with 
// n nodes using catalan
static int countBST(int n)
{
    // find nth catalan number
    int count = catalan(n);
 
    // return nth catalan number
    return count;
}
 
// A function to count number
// of binary trees with n nodes 
static int countBT(int n)
{
    // find count of BST
    // with n numbers
    int count = catalan(n);
 
    // return count * n!
    return count * factorial(n);
}
 
// Driver Code
static public void Main ()
{
    int count1, count2, n = 5;
     
    // find count of BST  
    // and binary trees 
    // with n nodes
    count1 = countBST(n);
    count2 = countBT(n); 
     
    // print count of BST and 
    // binary trees with n nodes
    Console.WriteLine("Count of BST with "+ 
                           n +" nodes is "+ 
                                   count1);
    Console.WriteLine("Count of binary " + 
                            "trees with "+ 
                        n + " nodes is " + 
                                   count2);
    }
}
 
// This code is contributed
// by akt_mit

PHP

<?php
// See https://www.geeksforgeeks.org/program-nth-catalan-number/
// for reference of below code.
// A function to find factorial
// of a given number
function factorial($n)
{
    $res = 1;
 
    // Calculate value of
    // [1*(2)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for ($i = 1; $i <= $n; ++$i)
    {
        $res *= $i;
    }
 
    return $res;
}
 
function binomialCoeff($n, $k)
{
    $res = 1;
 
    // Since C(n, k) = C(n, n-k)
    if ($k > $n - $k)
        $k = $n - $k;
 
    // Calculate value of 
    // [n*(n-1)*---*(n-k+1)] / 
    // [k*(k-1)*---*1]
    for ($i = 0; $i < $k; ++$i)
    {
        $res *= ($n - $i);
        $res = (int)$res / ($i + 1);
    }
 
    return $res;
}
 
// A Binomial coefficient 
// based function to find 
// nth catalan number in
// O(n) time
function catalan($n)
{
    // Calculate value of 2nCn
    $c = binomialCoeff(2 * $n, $n);
 
    // return 2nCn/(n+1)
    return (int)$c / ($n + 1);
}
 
// A function to count
// number of BST with 
// n nodes using catalan
function countBST($n)
{
    // find nth catalan number
    $count = catalan($n);
 
    // return nth 
    // catalan number
    return $count;
}
 
// A function to count 
// number of binary 
// trees with n nodes 
function countBT($n)
{
    // find count of 
    // BST with n numbers
    $count = catalan($n);
 
    // return count * n!
    return $count * 
           factorial($n);
}
 
// Driver Code
$count1;
$count2;
$n = 5;
 
// find count of BST and 
// binary trees with n nodes
$count1 = countBST($n);
$count2 = countBT($n); 
 
// print count of BST and 
// binary trees with n nodes
echo "Count of BST with " , $n ,
     " nodes is ", $count1,"\n";
      
echo "Count of binary trees with " , 
           $n ," nodes is ",$count2;
 
// This code is contributed by ajit
?>

Javascript

<script>
 
// See https://www.geeksforgeeks.org/program-nth-catalan-number/
// for reference of below code.
 
    // A function to find 
    // factorial of a given number
    function factorial(n)
    {
        let res = 1;
 
        // Calculate value of 
        // [1*(2)*---*(n-k+1)] / 
        // [k*(k-1)*---*1]
        for (let i = 1; i <= n; ++i)
        {
            res *= i;
        }
 
        return res;
    }
 
    function binomialCoeff(n, k)
    {
        let res = 1;
 
        // Since C(n, k) = C(n, n-k)
        if (k > n - k)
            k = n - k;
 
        // Calculate value of 
        // [n*(n-1)*---*(n-k+1)] / 
        // [k*(k-1)*---*1]
        for (let i = 0; i < k; ++i)
        {
            res *= (n - i);
            res /= (i + 1);
        }
 
        return res;
    }
 
    // A Binomial coefficient 
    // based function to find 
    // nth catalan number in 
    // O(n) time
    function catalan(n)
    {
 
        // Calculate value
        // of 2nCn
        let c = binomialCoeff(2 * n, n);
 
        // return 2nCn/(n+1)
        return c / (n + 1);
    }
 
    // A function to count 
    // number of BST with 
    // n nodes using catalan
    function countBST(n)
    {
        // find nth catalan number
        let count = catalan(n);
 
        // return nth catalan number
        return count;
    }
 
    // A function to count number
    // of binary trees with n nodes 
    function countBT(n)
    {
        // find count of BST
        // with n numbers
        let count = catalan(n);
 
        // return count * n!
        return count * factorial(n);
    }
       
    let count1, count2, n = 5;
       
    // find count of BST  
    // and binary trees 
    // with n nodes
    count1 = countBST(n);
    count2 = countBT(n); 
       
    // print count of BST and 
    // binary trees with n nodes
    document.write("Count of BST with "+ 
                           n +" nodes is "+ 
                                   count1 + "</br>");
    document.write("Count of binary " + 
                            "trees with "+ 
                        n + " nodes is " + 
                                   count2);
                                    
</script>

Output:

Count of BST with 5 nodes is 42
Count of binary trees with 5 nodes is 5040

Time Complexity: O(n): The time complexity of the above code is O(n). It uses the Catalan number formula to calculate the number of possible binary search trees in O(n) time.
Auxiliary Space Complexity: O(1), The space complexity of the above code is O(1). No extra space is allocated.

Proof of Enumeration

Consider all possible binary search trees with each element at the root. If there are n nodes, then for each choice of root node, there are n – 1 non-root nodes and these non-root nodes must be partitioned into those that are less than a chosen root and those that are greater than the chosen root.

Let’s say node i is chosen to be the root. Then there are i – 1 nodes smaller than i and n – i nodes bigger than i. For each of these two sets of nodes, there is a certain number of possible subtrees.

Let t(n) be the total number of BSTs with n nodes. The total number of BSTs with i at the root is t(i – 1) t(n – i). The two terms are multiplied together because the arrangements in the left and right subtrees are independent. That is, for each arrangement in the left tree and for each arrangement in the right tree, you get one BST with i at the root.

Summing over i gives the total number of binary search trees with n nodes.

$t(n) = \sum_{i=1}^{n} t(i-1) t(n-i)$

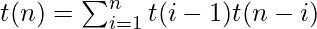
The base case is t(0) = 1 and t(1) = 1, i.e. there is one empty BST and there is one BST with one node.

$t(2) = t(0)t(1) + t(1)t(0) = 2$

$t(3) =t(0)t(2) +t(1)t(1) + t(2)t(0) = 2+1+2 = 5$

$t(4) = t(0)t(3) + t(1)t(2) +t(2)t(1)+ t(3)t(0) = 5+2+2+5 = 14$

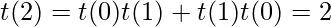
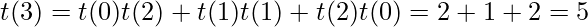
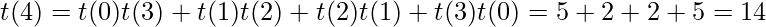
Also, the relationship countBT(n) = countBST(n) * n! holds. As for every possible BST, there can have n! binary trees where n is the number of nodes in BST.

Shubham Agarwal

Improve

Count the Number of Binary Search Trees present in a Binary Tree

Total number of possible Binary Search Trees and Binary Trees with n keys

C++

Java

Python3

C#

PHP

Javascript

Similar Reads

Please Login to comment...

What kind of Experience do you want to share?