Chapter 5 of the Class 9 NCERT Mathematics textbook introduces students to Euclid’s Geometry a foundational area of geometry that explores the axiomatic approach to understanding shapes, lines, and angles. Exercise 5.1 focuses on applying Euclid’s axioms and postulates to solve various problems and understand basic geometric concepts.
What is Euclid’s Geometry?
Euclid’s Geometry is a mathematical system attributed to the Greek mathematician Euclid often referred to as the “Father of Geometry”. It is based on a set of axioms and postulates that serve as the foundation for proving geometric propositions. Euclid’s most famous work, Elements, systematically presents these principles including the definitions, common notions, and geometric proofs. The system is characterized by its logical structure and deductive reasoning which forms the basis for classical geometry.
Question 1: Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There is an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
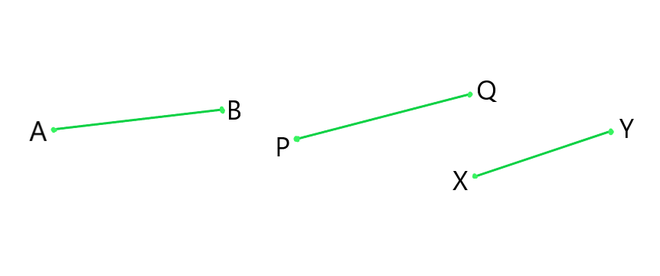
(v) In Given fig, if AB = PQ and PQ = XY, then AB = XY.
Solution:
(i) False
Reason: If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing through O.
(ii) False
Reason: Through two distinct points there can be only one line that can be drawn. Hence, the statement mentioned above is False.
(iii) True
Reason: A line that is terminated can be indefinitely produced on both sides as a line can be extended on both its sides infinitely. Hence, the statement mentioned above is True.
(iv) True
Reason: The radii of two circles are equal when the two circles are equal. The circumference and the centre of both the circles coincide; and thus, the radius of the two circles should be equal. Hence, the statement mentioned above is True.
(v) True
Reason: According to Euclid’s 1st axiom- “Things which are equal to the same thing are also equal to one another”. Hence, the statement mentioned above is True.
Question 2: Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line segment
(iv) Radius of a circle
(v) Square
Solution:
Yes, there are other terms which need to be defined first, so that we understand better:
- Plane: Flat surfaces in which geometric figures can be drawn are known are plane. A plane surface is a surface which lies evenly with the straight lines on itself.
- Point: A dimensionless dot which is drawn on a plane surface is known as point. A point is that which has no part.
- Line: A collection of points that has only length and no breadth is known as a line. And it can be extended on both directions. A line is breadth-less length.
(i) Parallel lines: Two lines l and m in a plan are said to be parallel if they have a no common point and we can write them as l || m.

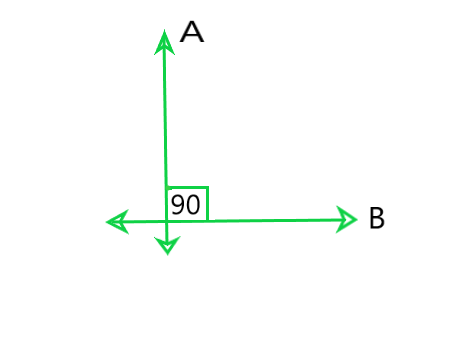
(ii) Perpendicular lines: Two lines A and B are said to be perpendicular if the form a right angle and we can write them as A ⊥ B.
(iii) Line Segment: A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points P and Q. Write it as arrow over PQ.

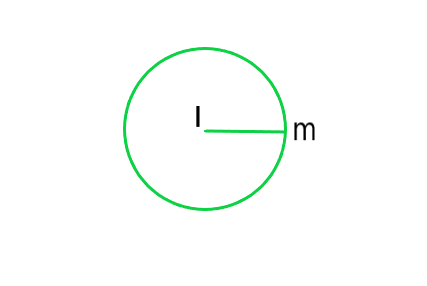
(iv) Radius of Circle: The distance from the centre to a point on the circle is called the radius of the circle. In the figure, l is centre and m is a point on the circle, then lm is the radius of the circle.
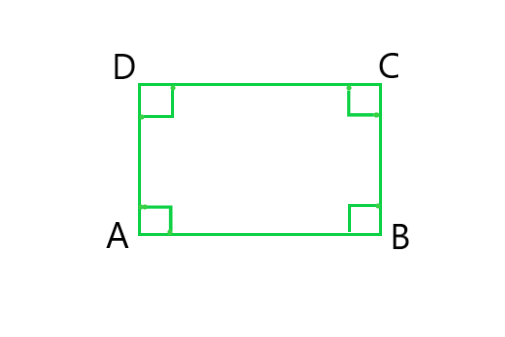
(v) Square: A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a Square
In the given figure ABCD is a Square.
Question 3: Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid’s postulates? Explain.
Solution:
Yes, these postulates contain undefined terms such as ‘Point and Line’. Undefined terms in the postulates are:
- There are many points that lie in a plane. But, in the postulates as given here, the position of the point C is not given, as of whether it lies on the line segment joining AB or it is not joining line segment.
- On top of that, there is no information about whether the points are in same plane or not.
And
Yes, these postulates are consistent when we deal with these two situations:
- Point C is lying on the line segment AB in between A and B.
- Point C does not lie on the line segment AB.
No, they don’t follow from Euclid’s postulates. They follow the axioms i.e “Given two distinct points, there is a unique line that passes through them.”
Question 4: If a point C lies between two points A and B such that AC = BC, then prove that AC = 12 AB, explain by drawing the figure.
Solution:
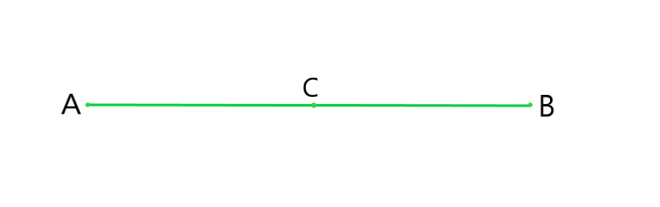
AC = BC (Given)
As we have studied in this chapter “If equals are added to equals then there wholes are also equal”.
Therefore, AC + BC = BC + AC
⇒ 2AC = BC+AC
As we have studied in this chapter, we know that,
BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal).
⇒ AC = (½)AB.
Question 5: In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Solution:
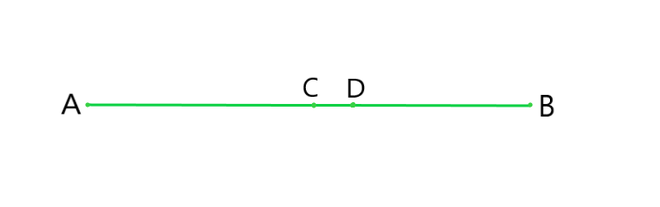
Let, AB be the line segment as given in the Question.
Assume that points C and D are the two different mid points of line segment AB.
Therefore, C and D are the midpoints of AB.
Now, as C and D are mid points of Ab we have,
AC = CB and AD = DB
CB+AC = AB (as it coincides with line segment AB)
Similarly, DB+AD = AB.
Now,
Adding AC to the L.H.S and R.H.S of the equation AC = CB
We get, AC+AC = CB+AC (If equals are added to equals, the wholes are equal.)
⇒ 2AC = AB — (i)
Similarly,
2 AD = AB — (ii)
From equation (i) and (ii), Since R.H.S are same, we equate the L.H.S we get,
2 AC = 2 AD (Things which are equal to the same thing are equal to one another.)
⇒ AC = AD (Things which are double of the same things are equal to one another.)
Thus, we conclude that C and D are the same points.
This contradicts our assumption that C and D are two different mid points of AB.
Thus, it is proved that every line segment has one and only one mid-point.
Hence, Proved.
Question 6: In Figure, if AC = BD, then prove that AB = CD.
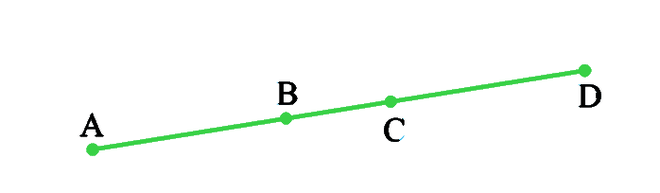
Solution:
According to the question, AC = BD
From the given figure we can conclude that,,
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD (AC = BD, given)
As we have studied, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S and R.H.S of the equation AB+BC = BC+CD, we get,
AB+BC-BC = BC+CD-BC
AB = CD
Hence Proved.
Question 7: Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate).
Solution:
Euclid’s fifth axiom states that “the whole is greater than the part.”
For Example: A cake. When it is whole or complete, assume that it measures 2 pounds but when a part from it is taken out and measured, its weight will be smaller than the previous measurement. So, the fifth axiom of Euclid is true for all the materials in the universe. Hence, Axiom 5, in the list of Euclid’s axioms, is considered a ‘universal truth’.
Conclusion
Understanding Euclid’s Geometry is crucial for the building a solid foundation in geometry. Exercise 5.1 provides an opportunity to the apply Euclid’s axioms and postulates to solve geometric problems enhancing students’ ability to the reason logically and understand geometric relationships. Mastery of these concepts is essential for the further studies in the mathematics and related fields.
FAQs on Introduction to Euclid’s Geometry
What are Euclid’s axioms?
The Euclid’s axioms are basic, self-evident truths that serve as the foundation for his geometric system. They are accepted without proof and include the concepts such as “A straight line can be drawn between any two points.”
What are the key postulates of Euclid’s geometry?
The Euclid’s postulates include the ideas such as “A straight line segment can be drawn joining any two points” and “All right angles are equal to one another”. These postulates help in forming the basis for the proving geometric theorems.
Why is Euclid’s geometry important?
The Euclid’s geometry is important because it provides the systematic and logical approach to the understanding geometric principles which has influenced mathematical thought and education for centuries.