NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry is an article curated by the professional team of subject matter experts at GfG, to help students learn how to solve the problems given in the NCERT textbook. NCERT Solutions for Class 9 Maths Chapter 5- Introduction to Euclid’s Geometry on this page are regularly revised and updated keeping the latest CBSE Syllabus in mind.
In Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry, students are introduced to an ancient branch of mathematics – ‘Euclid’s Geometry,’ and the NCERT Solutions provided here will help you understand the practical use of those concepts.
Introduction to Euclid’s Geometry is actually the foundation for basic geometry concepts and their applications. In NCERT Class 9 Chapter 5, you are going to learn about solids, planes, points, lines, curves, angles, circles, etc. based on the Euclidean axioms and postulates. Since geometry is a crucial part of Maths, it is important for students to understand this topic thoroughly and practice all the NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry given in their textbook.
NCERT Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry explains Euclid’s method of geometry, including the following topics:
The solutions to all the problems in Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry Exercises from the NCERT textbook have been covered in the NCERT Solutions for Class 9 Maths.
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry: Exercise 5.1
Question 1: Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There is an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In Given fig, if AB = PQ and PQ = XY, then AB = XY.
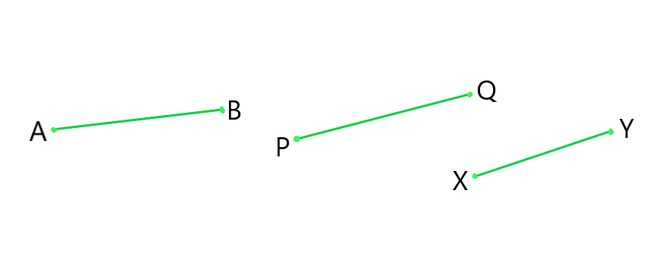
Solution:
(i) False
Reason: If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing through O.
(ii) False
Reason: Through two distinct points there can be only one line that can be drawn. Hence, the statement mentioned above is False.
(iii) True
Reason: A line that is terminated can be indefinitely produced on both sides as a line can be extended on both its sides infinitely. Hence, the statement mentioned above is True.
(iv) True
Reason: The radii of two circles are equal when the two circles are equal. The circumference and the centre of both the circles coincide; and thus, the radius of the two circles should be equal. Hence, the statement mentioned above is True.
(v) True
Reason: According to Euclid’s 1st axiom- “Things which are equal to the same thing are also equal to one another”. Hence, the statement mentioned above is True.
Question 2: Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line segment
(iv) Radius of a circle
(v) Square
Solution:
Yes, there are other terms which need to be defined first, so that we understand better:
- Plane: Flat surfaces in which geometric figures can be drawn are known are plane. A plane surface is a surface which lies evenly with the straight lines on itself.
- Point: A dimensionless dot which is drawn on a plane surface is known as point. A point is that which has no part.
- Line: A collection of points that has only length and no breadth is known as a line. And it can be extended on both directions. A line is breadth-less length.
(i) Parallel lines: Two lines l and m in a plan are said to be parallel if they have a no common point and we can write them as l || m.

(ii) Perpendicular lines: Two lines A and B are said to be perpendicular if the form a right angle and we can write them as A ⊥ B.
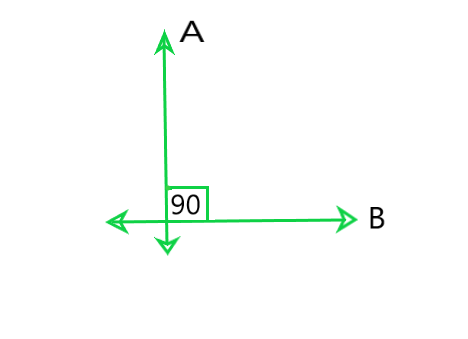
(iii) Line Segment: A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points P and Q. Write it as arrow over PQ.

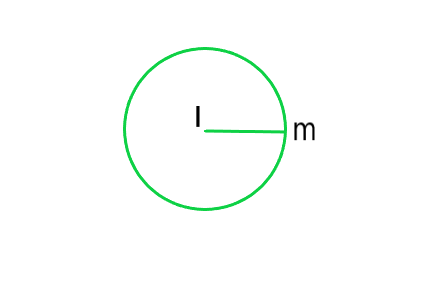
(iv) Radius of Circle: The distance from the centre to a point on the circle is called the radius of the circle. In the figure, l is centre and m is a point on the circle, then lm is the radius of the circle.
(v) Square: A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a Square
In the given figure ABCD is a Square.
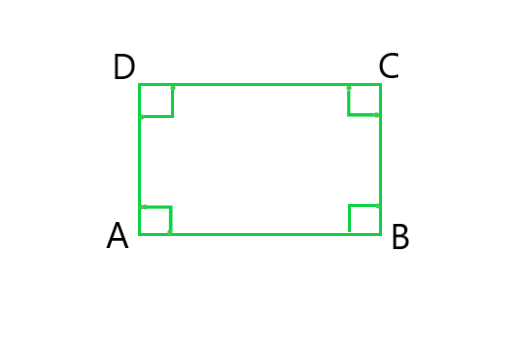
Question 3: Consider two ‘postulates’ given below:
- (i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
- (ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid’s postulates? Explain.
Solution:
Yes, these postulates contain undefined terms such as ‘Point and Line’. Undefined terms in the postulates are:
- There are many points that lie in a plane. But, in the postulates as given here, the position of the point C is not given, as of whether it lies on the line segment joining AB or it is not joining line segment.
- On top of that, there is no information about whether the points are in same plane or not.
And
Yes, these postulates are consistent when we deal with these two situations:
- Point C is lying on the line segment AB in between A and B.
- Point C does not lie on the line segment AB.
No, they don’t follow from Euclid’s postulates. They follow the axioms i.e “Given two distinct points, there is a unique line that passes through them.”
Question 4: If a point C lies between two points A and B such that AC = BC, then prove that AC = 12 AB, explain by drawing the figure.
Solution:
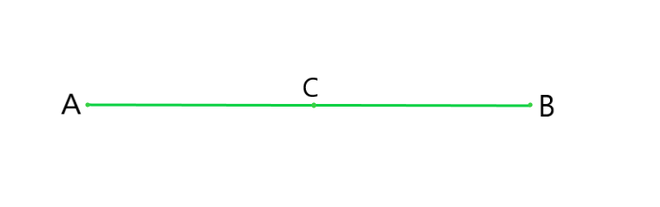
AC = BC (Given)
As we have studied in this chapter “If equals are added to equals then there wholes are also equal”.
Therefore, AC + BC = BC + AC
⇒ 2AC = BC+AC
As we have studied in this chapter, we know that,
BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal).
⇒ AC = (½)AB.
Question 5: In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Solution:
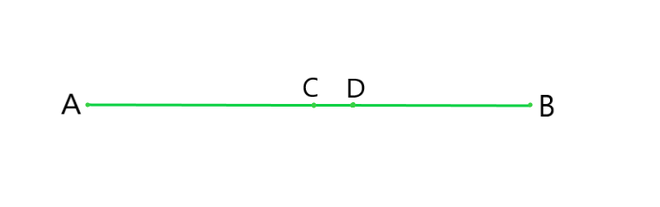
Let, AB be the line segment as given in the Question.
Assume that points C and D are the two different mid points of line segment AB.
Therefore, C and D are the midpoints of AB.
Now, as C and D are mid points of Ab we have,
AC = CB and AD = DB
CB+AC = AB (as it coincides with line segment AB)
Similarly, DB+AD = AB.
Now,
Adding AC to the L.H.S and R.H.S of the equation AC = CB
We get, AC+AC = CB+AC (If equals are added to equals, the wholes are equal.)
⇒ 2AC = AB — (i)
Similarly,
2 AD = AB — (ii)
From equation (i) and (ii), Since R.H.S are same, we equate the L.H.S we get,
2 AC = 2 AD (Things which are equal to the same thing are equal to one another.)
⇒ AC = AD (Things which are double of the same things are equal to one another.)
Thus, we conclude that C and D are the same points.
This contradicts our assumption that C and D are two different mid points of AB.
Thus, it is proved that every line segment has one and only one mid-point.
Hence, Proved.
Question 6: In Figure, if AC = BD, then prove that AB = CD.
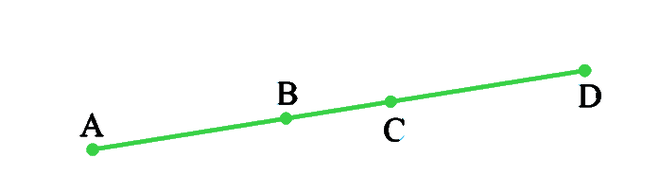
Solution:
According to the question, AC = BD
From the given figure we can conclude that,,
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD (AC = BD, given)
As we have studied, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S and R.H.S of the equation AB+BC = BC+CD, we get,
AB+BC-BC = BC+CD-BC
AB = CD
Hence Proved.
Question 7: Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate).
Solution:
Euclid’s fifth axiom states that “the whole is greater than the part.”
For Example: A cake. When it is whole or complete, assume that it measures 2 pounds but when a part from it is taken out and measured, its weight will be smaller than the previous measurement. So, the fifth axiom of Euclid is true for all the materials in the universe. Hence, Axiom 5, in the list of Euclid’s axioms, is considered a ‘universal truth’.
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry: Exercise 5.2
Question 1: How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Solution:
Euclid’s fifth postulate:
Euclid’s fifth postulate says that If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if the lines produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
i.e., the Euclid’s fifth postulate tell us about parallel lines.
Parallel lines are the lines which do not intersect each other ever and are always set at a perpendicular distance apart from each other.
Parallel lines can be two or more lines.
A: If X does not lie on the line A then we can draw a line through X which will be parallel to that of the line A.
B: There can be only one line that can be drawn through the point X which is parallel to the line A.
Therefore, Two distinct intersecting lines cannot be parallel to the same line.
Question 2: Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Solution:
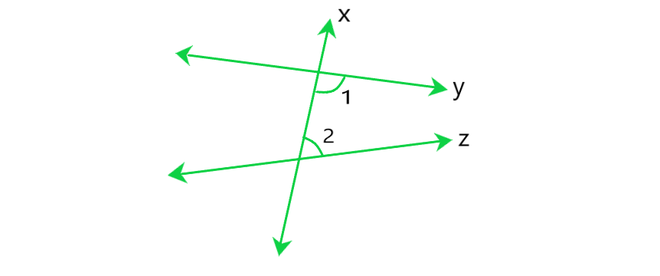
Yes. Euclid’s fifth postulate imply the existence of the parallel lines.
According to Euclid’s fifth postulate when a line x falls on a line y and z such that ∠1+ ∠2< 180°.
Then, line y and line z on producing further will meet in the side of ∠1 arid ∠2 which is less than 180°.
Therefore, we find that the lines which are not according to Euclid’s fifth postulate. i.e., ∠1 + ∠2 = 180°, do not intersect.
Key Features of NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry:
- These NCERT solutions are developed by the GFG team, with a focus on students’ benefit and for all the chapters of class 9 including Linear Equations in Two Variables.
- These solutions are entirely accurate and can be used by students to prepare for their board exams.
- All the solutions here are comprehensive and step-by-step so that students can solve all the problems with ease.
FAQs – NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry
1. Why is it important to learn about the Euclid’s Geometry?
Studying Euclid’s Geometry is important because it offers historical significance, develops logical reasoning and proof skills, introduces fundamental geometric concepts and relationships, enhances problem-solving abilities, and establishes a foundation for advanced mathematics. It allows students to appreciate the historical development of mathematical knowledge, apply deductive reasoning in constructing logical arguments, develop spatial reasoning skills, and tackle challenging geometric problems.
2. What topics are covered in NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry?
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry covers topics such as introduction to geometry, Euclid’s method of geometry and Euclid’s five postulates.
3. How can NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry help me?
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry can help you solve the NCERT exercise without any limitations. If you are stuck on a problem you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.
4. How many exercises are there in Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry?
There are 2 exercises in the Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry which covers all the important topics and sub-topics.
5. Where can I find NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry?
You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.